
科目: 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目: 来源: 题型:
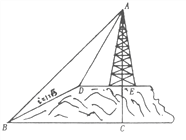
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数3.3 ,-2 ,0 ,![]() ,-3.5 ;
,-3.5 ;
(1) 比较这些数的绝对值的大小,并将这些数的绝对值用“>”号连接起来;
(2) 比较这些数的相反数的大小,并将这些数的相反数用“<”号连接起来.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1和图2,在△ABC中,AB=13,BC=14,![]() .
.
探究:如图1,AH⊥BC于点H,则AH=___,AC=___,△ABC的面积![]() =___.
=___.
拓展:如图2,点D在AC上(可与点A、C重合),分别过点A、C作直线BD的垂线,垂足为E、F,设BD=x,AE=m,CF=n,(当点D与A重合时,我们认为![]() =0).
=0).
(1)用含x、m或n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】把下列各数分别填入相应的集合里.
-4,![]() ,0,
,0,![]() ,-3.14,717,-(+5),+1.88,
,-3.14,717,-(+5),+1.88,![]()
(1)正数集合:{ … };
(2)负数集合:{ …};
(3)整数集合:{ …};
(4)分数集合:{ … }.
查看答案和解析>>
科目: 来源: 题型:
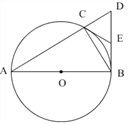
【题目】如图,已知ΔABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)若E是BD的中点,连结CE,试判断CE与⊙O的位置关系.
(2)若AC=3CD,求∠A的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校八年级学生全部参加“初二生物地理会考”,从中抽取了部分学生的生物考试成绩,将他们的成绩进行统计后分为A,B,C,D四等,并将统计结果绘制成如下的统计图,请结合图中所给的信息解答下列问题(说明:测试总人数的前30%考生为A等级,前30%至前70%为B等级,前70%至前90%为C等级,90%以后为D等级)

(1)抽取了 名学生成绩;
(2)请把频数分布直方图补充完整;
(3)扇形统计图中A等级所在的扇形的圆心角度数是 ;
(4)若测试总人数前90%为合格,该校初二年级有900名学生,求全年级生物合格的学生共约多少人.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们熟知的七巧板,是由宋代黄伯思设计的“燕几图”(“燕几”就是“宴几”,也就是宴请宾客的案几)演变而来.到了明代,严澄将“燕几图”里的方形案几改为三角形,发明了“蝶翅几”.而到了清代初期,在“燕几图”和“蝶翅几”的基础上,兼有三角形、正方形和平行四边形,能拼出更加生动、多样图案的七巧板就问世了(如图1网格中所示)
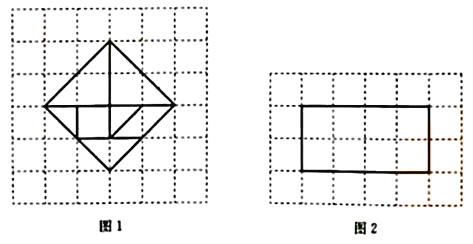
(1)若正方形网格的边长为1,则图1中七巧板的七块拼板的总面积为_____________
(2)使用图1中的七巧板可以拼出一个轮廓如图2所示的长方形,请在图2中画出拼图方法(要求:画出各块拼板的轮廓)
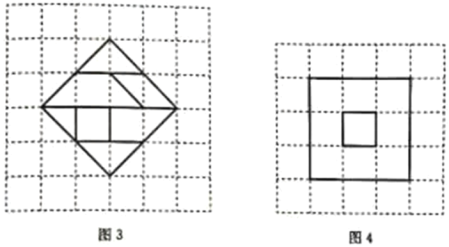
(3)随着七巧板的发展,出现了一些形式不同的七巧板,如图3所示的是另一种七巧板.利用图3中的七巧板可以拼出一个轮廓如图4所示的图形;大正方形的中间去掉一个小正方形,请在图4中画出拼图的方法(要求:画出各块拼板的轮廓)
查看答案和解析>>
科目: 来源: 题型:
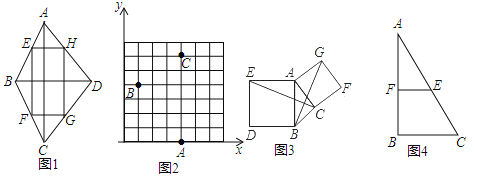
【题目】如图1,若顺次连接四边形ABCD各边中点得的四边形EFGH是矩形,则称原四边形ABCD为“中母矩形”即若四边形的对角线互相垂直,那么这个四边形称为“中母矩形”.
(1)如图2,在直角坐标系xOy中,已知A(4,0),B(1,4),C(4,6),请在格点上标出D点的位置(只标一点即可),使四边形ABCD是中母矩形.并写出点D的坐标.
(2)如图3,以△ABC的边AB,AC为边,向三角形外作正方形ABDE及ACFG,连接CE,BG相交于点O,试判断四边形BEGC是中母矩形?说明理由.
(3)如图4,在Rt△ABC中,AB=8,BC=6,E是斜边AC的中点,F是直角边AB的中点,P是直角边BC上一动点,试探究:当PC=_____时,四边形BPEF是中母矩形?(直角三角形中,30°角所对的直角边是斜边的一半)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com