
科目: 来源: 题型:
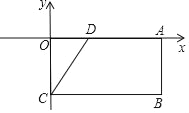
【题目】如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.
(1)求过点B、C、D的抛物线的解析式;
(2)求出(1)中抛物线与x轴的另一个交点E坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室.经预算,一共需要筹资30 000元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊.
(1)筹委会计划,购买书刊的资金不少于购买书桌、书架等设施资金的3倍,问最多用多少资金购买书桌、书架等设施?
(2)经初步统计,有200户居民自愿参与集资,那么平均每户需集资150元.镇政府了解情况后,赠送了一批阅览室设施和书籍,这样,只需参与户共集资20 000元.经筹委会进一步宣传,自愿参与的户数在200户的基础上增加了a%(其中![]() ).则每户平均集资的资金在150元的基础上减少了
).则每户平均集资的资金在150元的基础上减少了![]() %,求a的值.
%,求a的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校为使学生及时穿上合身的校服,现提前对该校八年级四班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为 6 个型号)

根据以上信息,解答下列问题(请写出每个空所需的求解步骤)
(1)该班共有多少名学生?其中穿 175 型号校服的学生有多少?
(2)在条形统计图中,请把空缺部分补充完整;(提醒:有两处需要补充)
(3)在扇形统计图中,185 型校服所对应的扇形圆心角的大小是 度;
(4)该班学生所穿校服型号的众数是 型,中位数是 型。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.

查看答案和解析>>
科目: 来源: 题型:
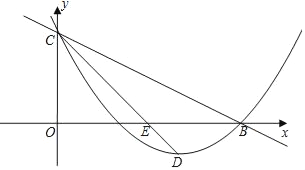
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
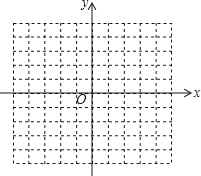
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
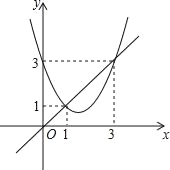
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,动点![]() 从
从![]() 出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点
出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点![]() 第
第![]() 次碰到矩形的边时,点
次碰到矩形的边时,点![]() 的坐标为( )
的坐标为( )

A. (0,3) B. (5,0) C. (1,4) D. (8,3)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.
查看答案和解析>>
科目: 来源: 题型:
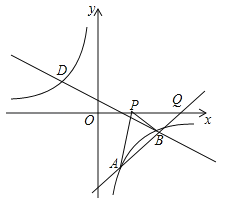
【题目】(2016湖北省黄冈市)如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
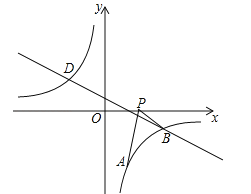
【答案】(1)y=x﹣4;(2)P(4,0).
【解析】试题分析:(1)先把A(1,a)代入反比例函数解析式求出a得到A点坐标,再解方程组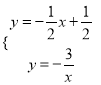 ,得B点坐标,然后利用待定系数法求AB的解析式;
,得B点坐标,然后利用待定系数法求AB的解析式;
(2)直线AB交x轴于点Q,如图,利用x轴上点的坐标特征得到Q点坐标,则PA﹣PB≤AB(当P、A、B共线时取等号),于是可判断当P点运动到Q点时,线段PA与线段PB之差达到最大,从而得到P点坐标.
试题解析:(1)把A(1,a)代入![]() 得a=﹣3,则A(1,﹣3),解方程组:
得a=﹣3,则A(1,﹣3),解方程组: 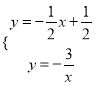 ,得:
,得: ![]() 或
或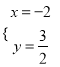 ,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得:
,则B(3,﹣1),设直线AB的解析式为y=kx+b,把A(1,﹣3),B(3,﹣1)代入得: ![]() ,解得:
,解得: ![]() ,所以直线AB的解析式为y=x﹣4;
,所以直线AB的解析式为y=x﹣4;
(2)直线AB交x轴于点Q,如图,当y=0时,x﹣4=0,解得x=4,则Q(4,0),因为PA﹣PB≤AB(当P、A、B共线时取等号),所以当P点运动到Q点时,线段PA与线段PB之差达到最大,此时P点坐标为(4,0).
考点:反比例函数与一次函数的交点问题.
【题型】解答题
【结束】
22
【题目】成都三圣乡花卉基地出售两种盆栽花卉:太阳花6元/盆,绣球花10元/盆.若一次购买的绣球花超过20盆时,超过20盆部分的绣球花价格打8折.
(1)若小张家花台绿化需用60盆两种盆栽花卉,小张爸爸给他460元钱去购买,问两种花卉各买了多少盆?
(2)分别写出两种花卉的付款金额y(元)关于购买量x(盆)的函数解析式;
(3)为了美化环境,花园小区计划到该基地购买这两种花卉共90盆,其中太阳花数量不超过绣球花数量的一半.两种花卉各买多少盆时,总费用最少,最少费用是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com