
科目: 来源: 题型:
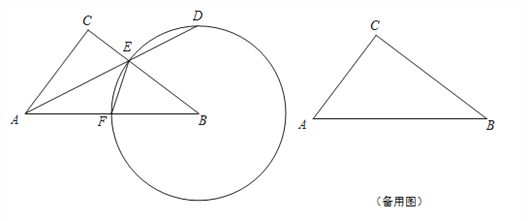
【题目】如图,已知在Rt△ABC中,∠ACB = 90o,AC =6,BC = 8,点F在线段AB上,以点B为圆心,BF为半径的圆交BC于点E,射线AE交圆B于点D(点D、E不重合).
(1)如果设BF = x,EF = y,求y与x之间的函数关系式,并写出它的定义域;
(2)如果![]() ,求ED的长;
,求ED的长;
(3)联结CD、BD,请判断四边形ABDC是否为直角梯形?说明理由.
查看答案和解析>>
科目: 来源: 题型:
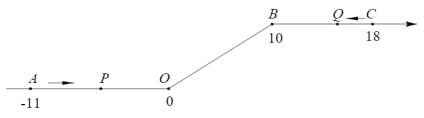
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条 “折线数轴” .图中点A表示-11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、B两点在数轴上相距的长度与Q、O两点在数轴上相距的长度相等.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与x轴交于点A和点B(1,0),与y轴相交于点C(0,3).
(1)求抛物线的解析式和顶点D的坐标;
(2)求证:∠DAB=∠ACB;
(3)点Q在抛物线上,且△ADQ是以AD为底的等腰三角形,求Q点的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)求△ABC的面积;
(3)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.

查看答案和解析>>
科目: 来源: 题型:
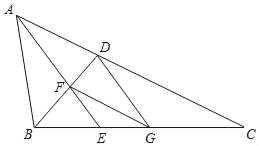
【题目】如图,已知在△ABC中,∠BAC=2∠C,∠BAC的平分线AE与∠ABC的平分线BD相交于点F,FG∥AC,联结DG.
(1)求证:BFBC=ABBD;
(2)求证:四边形ADGF是菱形.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了响应上海市市政府“绿色出行”的号召,减轻校门口道路拥堵的现状,王强决定改父母开车接送为自己骑车上学.已知他家离学校7.5千米,上下班高峰时段,驾车的平均速度比自行车平均速度快15千米/小时,骑自行车所用时间比驾车所用时间多![]() 小时,求自行车的平均速度?
小时,求自行车的平均速度?
查看答案和解析>>
科目: 来源: 题型:
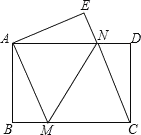
【题目】如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,ND=1.
①求MC的长.
②求MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数![]() 的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o,
的图像与x轴、y轴分别交于点A、B,以AB为边在第一象限内作直角三角形ABC,且∠BAC = 90o, ![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)在第一象限内有一点M(1,m),且点M与点C位于直线AB的同侧,使得![]() ,求点M的坐标.
,求点M的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】(![]() )探究发现
)探究发现
下面是一道例题及其解答过程,请补充完整:
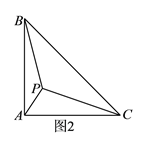
如图①在等边![]() 内部,有一点
内部,有一点![]() ,若
,若![]() ,求证:
,求证: ![]() ,
,
证明:将![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,则
,则![]() 为等边三角形.
为等边三角形.
∴![]() ,
, ![]() ,
, ![]() __________.
__________.
∵![]() ,∴
,∴![]() ,
,
∴![]() __________,
__________,
即![]() ,
,
(![]() )类比延伸:
)类比延伸:
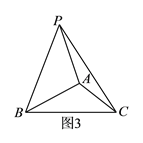
如图②在等腰三角形![]() 中,
中, ![]() ,内部有一点
,内部有一点![]() ,若
,若![]() ,试判断线段
,试判断线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
(![]() )联想拓展:
)联想拓展:
如图③在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上方,且
上方,且![]() ,满足
,满足![]() ,请直接写出
,请直接写出![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com