
科目: 来源: 题型:
【题目】如图,已知四边形ABCD和直线MN,点O在直线MN上.
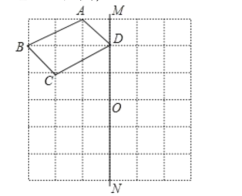
(1)画出四边形![]() 使四边形
使四边形![]() 与四边形ABCD关于直线MN成轴对称;
与四边形ABCD关于直线MN成轴对称;
(2)画出四边形![]() 使四边形
使四边形![]() 与四边形ABCD关于点O对称:
与四边形ABCD关于点O对称:
(3)四边形![]() 和四边形
和四边形![]() 是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心.
是轴对称和中心对称吗?若是,请在图上画出对称轴或对称中心.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知长方形ABCD,点E在线段AD上,将![]() 沿直线BE翻折后,点A落在线段CD上的点F.如果
沿直线BE翻折后,点A落在线段CD上的点F.如果![]() 的周长为12,
的周长为12,![]() 的周长为24,那么FC长为________.
的周长为24,那么FC长为________.
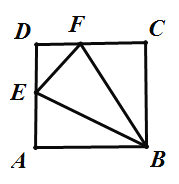
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在长方形ABCD中,![]() ,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
,将长方形ABCD绕点D逆时针旋转90°,点A、B、C分别对应点E、F、G.
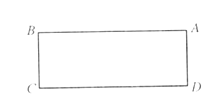
(1)画出长方形EFGD;
(2)连接BD、DF、BF,请用含有a、b的代数式表示![]() 的面积;
的面积;
(3)如果BF交CD于点H,请用含有a、b的代数式表示CH的长度.
查看答案和解析>>
科目: 来源: 题型:
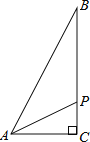
【题目】在![]() 中,
中,![]() ,点P从点A出发,以
,点P从点A出发,以![]() 的速度沿折线
的速度沿折线![]() 运动,最终回到点A,设点P的运动时间为
运动,最终回到点A,设点P的运动时间为![]() ,线段AP的长度为
,线段AP的长度为![]() ,则能够反映y与x之间函数关系的图象大致是
,则能够反映y与x之间函数关系的图象大致是![]()
A. 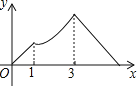 B.
B. 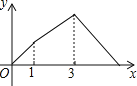
C. 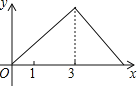 D.
D. 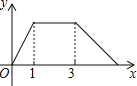
查看答案和解析>>
科目: 来源: 题型:
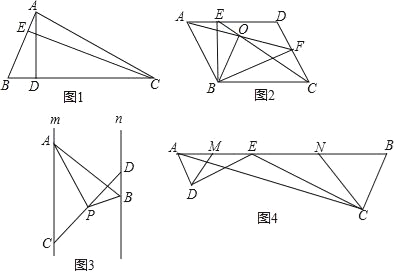
【题目】【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ABC中,AB=3,AD=6,问△ABC的高AD与CE的比是多少?
小聪的计算思路是:
根据题意得:S△ABC=![]() BCAD=
BCAD=![]() ABCE.
ABCE.
从而得2AD=CE,∴![]()
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在ABCD中,点E、F分别在AD,CD上,且AF=CE,并相交于点O,连接BE、BF,
求证:BO平分角AOC.
(2)【探究延伸】
如图3,已知直线m∥n,点A、C是直线m上两点,点B、D是直线n上两点,点P是线段CD中点,且∠APB=90°,两平行线m、n间的距离为4.求证:PAPB=2AB.
(3)【迁移应用】
如图4,E为AB边上一点,ED⊥AD,CE⊥CB,垂足分别为D,C,∠DAB=∠B,AB=![]() ,BC=2,AC=
,BC=2,AC=![]() ,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分c1与经过点A、D、B的抛物线的一部分c2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,﹣![]() ),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
),点M是抛物线C2:y=mx2﹣2mx﹣3m(m<0)的顶点.
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求m的值.

查看答案和解析>>
科目: 来源: 题型:
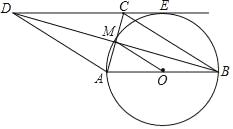
【题目】如图,四边形ABCD中,MA=MC,MB=MD,以AB为直径的O过点M且与DC延长线相切于点E.
(1)求证:四边形ABCD是菱形;
(2)若AB=4,求![]() 的长(结果请保留π)
的长(结果请保留π)
查看答案和解析>>
科目: 来源: 题型:
【题目】新能源汽车环保节能,越来越受到消费者的喜爱.各种品牌相继投放市场.一汽贸公司经销某品牌新能源汽车.去年销售总额为5000万元,今年1~5月份,每辆车的销售价格比去年降低1万元.销售数量与去年一整年的相同.销售总额比去年一整年的少20%,今年1~5月份每辆车的销售价格是多少万元?设今年1~5月份每辆车的销售价格为x万元.根据题意,列方程正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).
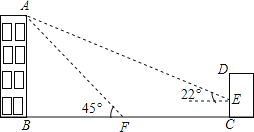
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com