
科目: 来源: 题型:
【题目】某食品厂从生产的袋装食品中抽出样品20袋,以每袋标准质量45克为标准,检测每袋的质量是否符合该标准,超过或不足的克数分别用正、负数来表示,记录如下:
与标准质量的差值(单位:克) | ﹣5 | ﹣3 | 0 | 1 | 2 | 5 |
袋数 | 1 | 3 | 6 | 4 | 5 | 1 |
回答下列问题:
(1)这20袋样品中,完全符合每袋标准质量45克的有 袋;
(2)这批样品的总质量是多少克?(要求写出算式).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知E、F、G、H分别是矩形四边AB、BC、CD、DA的中点,且四边形EFGH的周长为16cm,则矩形ABCD的对角线长等于________cm.

查看答案和解析>>
科目: 来源: 题型:
【题目】小张去水果市场购买苹果和桔子,他看中了 A 、B 两家的苹果和桔子,这两家的苹果和桔子的品质都一样,售价也相同,但每千克苹果要比每千克桔子多 12 元,买 2 千克苹果与买 5 千克桔子的费用相等.
(1)根据题意列出方程;
(2)在 x=6,x=7,x=8 中,哪一个是(1)中所列方程的解;
(3)经洽谈,A 家优惠方案是:每购买 10 千克苹果,送 1 千克桔子;B 家优惠方案是:若购买苹果超过 5 千克,则购买桔子打八折,设每千克桔子 x 元, 假设小张购买 30 千克苹果和 a 千克桔子(a>5).
①请用含 a 的式子分别表示出小张在 A、B 两家购买苹果和桔子所花的费用;
②若 a=16,你认为在哪家购买比较合算?
查看答案和解析>>
科目: 来源: 题型:
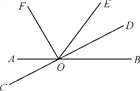
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,……以此类推,则a2018的值为( )
A. ﹣1007 B. ﹣1008 C. ﹣1009 D. ﹣2018
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AB=4![]() ,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )
,F是线段AC上一点,过点A的⊙F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 ( )

A. 3![]() B. 2
B. 2![]() C.
C. ![]() D. 2
D. 2
查看答案和解析>>
科目: 来源: 题型:
【题目】河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为:15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )
A. 中位数是12.7% B. 众数是15.3%
C. 平均数是15.98% D. 方差是0
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC三个顶点A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转使A落在y轴上,与此同时顶点C恰好落在![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
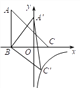
A. -2 B. -3 C. -4 D. -5
查看答案和解析>>
科目: 来源: 题型:
【题目】(定义新知)在数轴上,点M和点N分别表示数x1和x2 ,可以用绝对值表示点M、N两点间的距离d (M,N),即d (M,N)=|x1-x2|.
(初步应用)
(1)在数轴上,点A、B、C分别表示数-1、2、x, 解答下列问题:
①d (A,B)= ;
②若d(A,C)=2,则x的值为 ;
③若d(A,C)+d(B,C)=d(A,B),且x为整数,则x的取值有 个.
(综合应用)
(2)在数轴上,点D、E、F分别表示数-2、4、6.动点P沿数轴从点D开始运动,到达F点后立刻返回,再回到D点时停止运动.在此过程中,点P的运动速度始终保持每秒2个单位长度.设点P的运动时间为t秒.
①当t= 时,d(D,P)=3;
②在整个运动过程中,请用含t的代数式表示d(E,P).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,O为原点,ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(﹣2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.
(1)求抛物线的解析式;
(2)求证:DE是⊙P的切线;
(3)若将△CDE绕点D顺时针旋转90°,点E的对应点E′会落在抛物线y=ax2+bx+c上吗?请说明理由;
(4)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B、D、M、N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com