
科目: 来源: 题型:
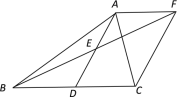
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF.
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
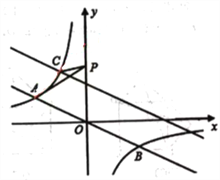
【题目】如图,直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点,已知A点的纵坐标是2.
的图象交于A,B两点,已知A点的纵坐标是2.
(1)求反比例函数的解析式.
(2)将直线![]() 沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
沿x轴向右平移6个单位后,与反比例函数在第二象限内交于点C.动点P在y轴正半轴上运动,当线段PA与线段PC之差达到最大时,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
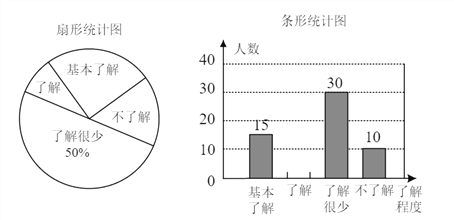
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____.
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
【答案】(1)60;90°;(2)补图见解析;(3)300;(4)![]()
【解析】分析:(1)根据了解很少的人数除以了解很少的人数所占的百分百求出抽查的总人数,再用“基本了解”所占的百分比乘以360°,即可求出“基本了解”部分所对应扇形的圆心角的度数;(2)用调查的总人数减去“基本了解”“了解很少”和“基本了解”的人数,求出了解的人数,从而补全统计图;(3)用总人数乘以“了解”和“基本了解”程度的人数所占的比例,即可求出达到“了解”和“基本了解”程度的总人数;(4)根据题意列出表格,再根据概率公式即可得出答案.
详解:(1)60;90°.
(2)补全的条形统计图如图所示.
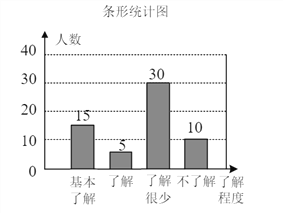
(3)对食品安全知识达到“了解”和“基本了解”的学生所占比例为![]() ,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为
,由样本估计总体,该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数为![]() .
.
(4)列表法如表所示,
男生 | 男生 | 女生 | 女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
男生 | 男生男生 | 男生女生 | 男生女生 | |
女生 | 男生女生 | 男生女生 | 女生女生 | |
女生 | 男生女生 | 女生女生 |
所有等可能的情况一共12种,其中选中1个男生和1个女生的情况有8种,所以恰好选中1个男生和1个女生的概率是![]() .
.
点睛:本题考查了条形统计图、扇形统计图以及用列表法或树状图法求概率,根据题意求出总人数是解题的关键;注意运用概率公式:概率=所求情况数与总情况数之比.
【题型】解答题
【结束】
24
【题目】为响应国家全民阅读的号召,某社区鼓励居民到社区阅览室借阅读书,并统计每年的借阅人数和图书借阅总量(单位:本),该阅览室在2015年图书借阅总量是7500本,2017年图书借阅总量是10800本.
(1)求该社区的图书借阅总量从2015年至2017年的年平均增长率.
(2)已知2017年该社区居民借阅图书人数有1350人,预计2018年达到1440人,如果2017年至2018年图书借阅总量的增长率不低于2015年至2017年的年平均增长率,设2018年的人均借阅量比2017年增长a%,求a的值至少是多少?
查看答案和解析>>
科目: 来源: 题型:
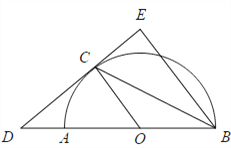
【题目】如图,已知![]() 是
是![]() 的直径,CD与
的直径,CD与![]() 相切于C,
相切于C, ![]() .
.
(1)求证:BC 是![]() 的平分线.
的平分线.
(2)若DC=8, ![]() 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.
【答案】(1)证明见解析;(2)4.8
【解析】分析:(1)由![]() ,推出
,推出![]() ,由
,由![]() ,推出
,推出![]() ,可得
,可得![]() .(2)在
.(2)在![]() 中,求出OD,由
中,求出OD,由![]() ,可得
,可得![]() ,由此即可解决问题.
,由此即可解决问题.
详解:(1)证明:因为![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
故可得![]() ,
,
即可得![]() 是
是![]() 的平分线.
的平分线.
(2)因为DE是![]() 的切线,
的切线,
所以![]() ,即在
,即在![]() 中,DC=8,OC=OA=6,所以
中,DC=8,OC=OA=6,所以![]() ,
,
又因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
即可得EC=4.8
点睛:本题主要考查了切线的性质及相似三角形的应用,题目难度适中,会综合运用所考查的知识点是解题的关键.
【题型】解答题
【结束】
23
【题目】“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
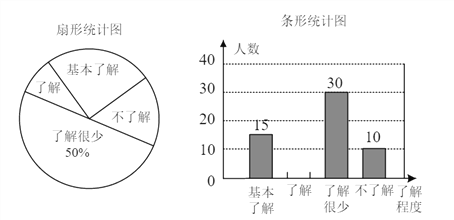
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____.
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目: 来源: 题型:
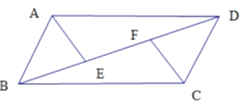
【题目】如图,在口ABCD中,点E、F是对角线BD上的两点,且BF=DE,连接AE、CF.
.求证:AE//CF.
【答案】证明见解析
【解析】试题分析:根据平行四边形的性质可得AD=CB,∠ADE=∠CBF,利用SAS判定△ADE≌△CBF,根据全等三角形的性质即可得∠AED=∠BFC,所以AE∥CF.
试题解析:
∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠ADE=∠CBF,
又∵DE=BF,
∴△ADE≌△CBF,
∴∠AED=∠BFC,
∴AE∥CF.
【题型】解答题
【结束】
22
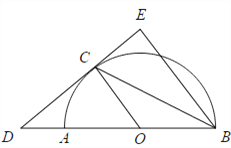
【题目】如图,已知![]() 是
是![]() 的直径,CD与
的直径,CD与![]() 相切于C,
相切于C, ![]() .
.
(1)求证:BC 是![]() 的平分线.
的平分线.
(2)若DC=8, ![]() 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
【答案】②③
【解析】分析:(1)根据题目中给的计算方法代入计算后判定即可;(2)根据题目中给的计算方法代入计算后判定即可;(3)根据题目中给的计算方法代入计算后判定即可;(4)结合x的取值范围,分类讨论,利用题目中给出的方法计算后判定即可.
详解:
①当x=1.7时,
[x]+(x)+[x)
=[1.7]+(1.7)+[1.7)=1+2+2=5,故①错误;
②当x=﹣2.1时,
[x]+(x)+[x)
=[﹣2.1]+(﹣2.1)+[﹣2.1)
=(﹣3)+(﹣2)+(﹣2)=﹣7,故②正确;
③当1<x<1.5时,
4[x]+3(x)+[x)
=4×1+3×2+1
=4+6+1
=11,故③正确;
④∵﹣1<x<1时,
∴当﹣1<x<﹣0.5时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当﹣0.5<x<0时,y=[x]+(x)+x=﹣1+0+x=x﹣1,
当x=0时,y=[x]+(x)+x=0+0+0=0,
当0<x<0.5时,y=[x]+(x)+x=0+1+x=x+1,
当0.5<x<1时,y=[x]+(x)+x=0+1+x=x+1,
∵y=4x,则x﹣1=4x时,得x=![]() ;x+1=4x时,得x=
;x+1=4x时,得x=![]() ;当x=0时,y=4x=0,
;当x=0时,y=4x=0,
∴当﹣1<x<1时,函数y=[x]+(x)+x的图象与正比例函数y=4x的图象有三个交点,故④错误,
故答案为:②③.
点睛:本题是阅读理解题,前三问比较容易判定,根据题目所给的方法判定即可;第四问较难,结合x的取值范围分情况讨论即可.
【题型】填空题
【结束】
19
【题目】先化简再求值: ![]() ,其中
,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学有若干套损坏的桌椅,现有甲、乙两名木工,甲每天可以修桌椅16套,乙每天比甲多修桌椅8套,甲单独修完这些桌椅比乙单独修完多用10天,学校每天付甲80元修理费,付乙120元修理费.
(1)这批损坏的桌椅有多少套?(列方程解答)
(2)在修理过程中,学校要派一名工作人员进行质量监督,学校负担他每天30元生活补助费,现有两种修理方案:
①由乙单独修理;
②甲、乙合作同时修理.
你认为哪种方案省钱?试通过计算说明.
查看答案和解析>>
科目: 来源: 题型:
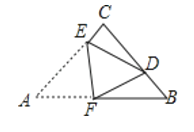
【题目】如图,在△ABC中, ![]() , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则![]() 的值为_____________.
的值为_____________.
【答案】![]()
【解析】分析:过点D作DG![]() AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
在Rt△DCE中,由勾股定理求得![]() ,所以DB=
,所以DB=![]() ;在Rt△ABC中,由勾股定理得
;在Rt△ABC中,由勾股定理得![]() ;在Rt△DGB中,由锐角三角函数求得
;在Rt△DGB中,由锐角三角函数求得![]() ,
, ![]() ;
;
设AF=DF=x,则FG= ![]() ,在Rt△DFG中,根据勾股定理得方程
,在Rt△DFG中,根据勾股定理得方程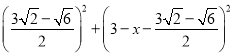 =
=![]() ,解得
,解得![]() ,从而求得
,从而求得![]() .的值
.的值
详解:
如图所示,过点D作DG![]() AB于点G.
AB于点G.

根据折叠性质,可知△AEF![]() △DEF,
△DEF,
∴AE=DE=2,AF=DF,CE=AC-AE=1,
在Rt△DCE中,由勾股定理得![]() ,
,
∴DB=![]() ;
;
在Rt△ABC中,由勾股定理得![]() ;
;
在Rt△DGB中, ![]() ,
, ![]() ;
;
设AF=DF=x,得FG=AB-AF-GB=![]() ,
,
在Rt△DFG中, ![]() ,
,
即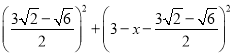 =
=![]() ,
,
解得![]() ,
,
∴![]() =
=![]() =
=![]() .
.
故答案为: ![]() .
.
点睛:主要考查了翻折变换的性质、勾股定理、锐角三件函数的定义;解题的关键是灵活运用折叠的性质、勾股定理、锐角三角函数的定义等知识来解决问题.
【题型】填空题
【结束】
18
【题目】规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com