
科目: 来源: 题型:
【题目】已知代数式A=x2+3xy+x﹣12,B=2x2﹣xy+4y﹣1
(1)当x=y=﹣2时,求2A﹣B的值;
(2)若2A﹣B的值与y的取值无关,求x的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在研究位似问题时,甲、乙同学的说法如下:
甲:如图①,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(﹣4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为(0,2).


图① 图②
乙:如图②,正方形网格中,每个小正方形的边长是1个单位长度,以点C为位似中心,在网格中画△A1B1C1,使△A1B1C1与△ABC位似,且△A1B1C1与△ABC的位似比为2:1,则点B1的坐标为(4,0).
对于两人的观点,下列说法正确的是( )
A. 两人都对 B. 两人都不对 C. 甲对乙不对 D. 甲不对乙对
查看答案和解析>>
科目: 来源: 题型:
【题目】在学校组织的知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
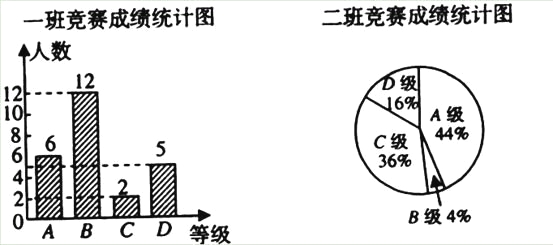
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在C级以上(包括C级)的人数为_______;
(2)请你将表格补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 | 87.6 | 90 | |
二班 | 87.6 | 100 |
(3)请从下列不同角度对这次竞赛成绩的结果进行
①从平均数和中位数的角度来比较一班和二班的成绩;
②从平均数和众数的角度来比较一班和二班的成绩;
③从B级以上(包括B级)的人数的角度来比较一班和二班的成绩.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3![]()
(1)直接写出点B的坐标
(2)已知D.E分别为线段OC.OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式
(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O.D.M.N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由。

查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究问题背景数学活动课上,老师将一副三角尺按图(1)所示位置摆放,分别作出∠AOC,∠BOD的平分线OM、ON,然后提出如下问题:求出∠MON的度数.
特例探究“兴趣小组”的同学决定从特例入手探究老师提出的问题,他们将三角尺分别按图2、图3所示的方式摆放,OM和ON仍然是∠AOC和∠BOD的角平分线.其中,按图2方式摆放时,可以看成是ON、OD、OB在同一直线上.按图3方式摆放时,∠AOC和∠BOD相等.
(1)请你帮助“兴趣小组”进行计算:图2中∠MON的度数为 °.图3中∠MON的度数为 °.
发现感悟
解决完图2,图3所示问题后,“兴趣小组”又对图1所示问题进行了讨论:
小明:由于图1中∠AOC和∠BOD的和为90°,所以我们容易得到∠MOC和∠NOD的和,这样就能求出∠MON的度数.
小华:设∠BOD为x°,我们就能用含x的式子分别表示出∠NOD和∠MOC度数,这样也能求出∠MON的度数.
(2)请你根据他们的谈话内容,求出图1中∠MON的度数.
类比拓展
受到“兴趣小组”的启发,“智慧小组”将三角尺按图4所示方式摆放,分别作出∠AOC、∠BOD的平分线OM、ON,他们认为也能求出∠MON的度数.
(3)你同意“智慧小组”的看法吗?若同意,求出∠MON的度数;若不同意,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价l80元,售价320元;乙种服装每件进价l50元,售价280元.
(1)若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?
(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0<a<20)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面内有一等腰直角三角板(∠ACB=90)和直线l.过点C作CE⊥l于点E,过点B作BF⊥l于点F.当点E与点A重合时(图①),易证:AF+BF=2CE.当三角板绕点A顺时针旋转至图②.图③的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,请直接写出线段AF.BF.CE之间的数量关系的猜想(不需证明).
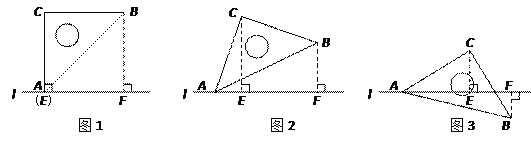
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,4),B(3,2),C(6,3).

(1)画出△ABC关于x轴对称的△A![]() B
B![]() C
C![]() ;
;
(2)以M点为位似中心,在网格中画出△A![]() B
B![]() C
C![]() 的位似图形△A
的位似图形△A![]() B
B![]() C
C![]() ,使△A2B2C2与△A
,使△A2B2C2与△A![]() B
B![]() C
C![]() 的相似比为2:1.
的相似比为2:1.
(3)请写出(2)中放大后的△A![]() B
B![]() C
C![]() 中A
中A![]() B
B![]() 边的中点P的坐标.
边的中点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com