
科目: 来源: 题型:
【题目】阅读以下证明过程:
已知:在△ABC中,∠C≠90°,设AB=c,AC=b,BC=a.求证:a2+b2≠c2.
证明:假设a2+b2=c2,则由勾股定理逆定理可知∠C=90°,这与已知中的∠C≠90°矛盾,故假设不成立,所以a2+b2≠c2.
请用类似的方法证明以下问题:
已知:关于x的一元二次方程x2﹣(m+1)x+2m-3=0 有两个实根x1和x2.
求证:x1≠x2.

查看答案和解析>>
科目: 来源: 题型:
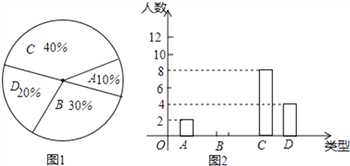
【题目】某校要求200名学生进行社会调查,每人必须完成3~6份报告,调查结束后随机抽查了20名学生每人完成报告的份数,并分为四类,A:3份;B:4份;C:5份;D:6份.将各类的人数绘制成扇形图(如图1)和尚未完整的条形图(如图2),回答下列问题:
(1)请将条形统计图2补充完整;
(2)写出这20名学生每天完成报告份数的众数_____份和中位数_____份;
(3)在求出20名学生每人完成报告份数的平均数时,小明是这样分析的:
第一步:求平均数的公式是 ![]() =
=![]() ;
;
第二步:在该问题中,n=4,x1=3,x2=4,x3=5,x4=6;
第三步:![]() =
=![]() =4.5(份).
=4.5(份).
小明的分析对不对?如果对,请说明理由,如果不对,请求出正确结果;
(4)现从“D类”的学生中随机选出2人进行采访,若“D类”的学生中只有1名男生,则所选两位同学中有男同学的概率是多少?请用列表法或树状图的方法求解.
查看答案和解析>>
科目: 来源: 题型:
【题目】(阅读理解)小海喜欢研究数学问题,在计算整式加减(﹣4x2﹣7+5x)+(2x+3x2)的时候,想到了小学的列竖式加减法,令A=﹣4x2﹣7+5x,B=2x+3x2,然后将两个整式关于x进行降幂排列,A=﹣4x2+5x﹣7,B=3x2+2x,最后只要写出其各项系数对齐同类项进行竖式计算如下:
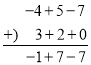
所以,(﹣4x2﹣7+5x)+(2x+3x2)=﹣x2+7x﹣7.
(模仿解题)若A=﹣4x2y2+2x3y﹣5xy3+2x4,B=3x3y+2x2y2﹣y4﹣4xy3,请你按照小海的方法,先对整式A,B关于某个字母进行降幂排列,再写出其各项系数进行竖式计算A﹣B,并写出A﹣B的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知命题“若 a>b,则 a2>b2”.
(1)此命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出一个 反例.
(2)写出此命题的逆命题,并判断此逆命题的真假;若是真命题,请给予证明;若是假 命题,请举出一个反例.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图,已知∠BOC:∠AOC=4:1,OD平分∠AOB,且∠COD=39°,求∠AOB的度数.

(2)2019年11月份,我县教体局由县城老区搬到了新区(海丰16路与棣新4路交叉口),当时某科室需要把相关档案由老区办公楼搬到新区办公楼,如果让甲搬家公司需要8天完成;如果由乙搬家公司需要6天完成。现在甲搬家公司工作一天后,为加快进度,由两搬家公司一块儿工作,搬完剩下的档案。问搬完这些档案一共需要多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等腰梯形 ABCD 中,AD∥BC,AB=CD.点 P 为底边 BC 的延长线上任意一点,PE⊥AB 于 E,PF⊥DC 于 F,BM⊥DC 于 M.请你探究线段 PE、PF、BM 之间的数量关系:
______.

查看答案和解析>>
科目: 来源: 题型:
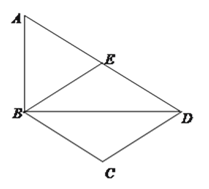
【题目】如图,在Rt△ABD中,∠ABD=90°,AB=1,sin∠ADB=![]() ,点E为AD的中点,线段BA绕点B顺时针旋转到BC(旋转角小于180°),使BC∥AD.连接DC,BE.
,点E为AD的中点,线段BA绕点B顺时针旋转到BC(旋转角小于180°),使BC∥AD.连接DC,BE.
(1)则四边形BCDE是________,并证明你的结论;
(2)求线段AB旋转过程中扫过的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() ,过点A(1,-3)作直线l∥y轴,交抛物线
,过点A(1,-3)作直线l∥y轴,交抛物线![]() 于点B,交抛物线
于点B,交抛物线![]() 于点C,则以下结论:
于点C,则以下结论:
(1)抛物线![]() 与 y轴的交点坐标为(0,1)
与 y轴的交点坐标为(0,1)
(2)若点D(-4,m)及点E(7,n)均在抛物线![]() 上,则m>n;
上,则m>n;
(3)若点B在点A的上方,则c>0;
(4)若BC=2,则c=3;
其中结论正确的是( )

A. (1)(2) B. (2)(3) C. (3)(4) D. (1)(4)
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)计算:![]()
(2)如图,延长线段AB至C使BC=2AB,延长线段BA至D使AD=3AB,点E是线段DB的中点,点F是线段AC的中点,若AB=6cm,求EF的长度.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)把一堆黑色棋子按如图1所示的规律排列起来,摆成第n个“口”需要a枚黑色的棋子,请用含n的代数式表示:a=
图1;

(2)把一堆黑色和白色棋子按如图2所示的规律排列起来:

求:从前往后数,第2018颗棋子的颜色。
(3)把一堆黑色和白色棋子被按如图3所示的规律排列起来:

若图3中的黑色棋子全部由图1中的a枚黑色棋子充当,用完为止(黑色棋子共有a枚),按照这样的规律摆放至以黑色棋子收尾。当a=100,请列式并计算:这时,图3中黑白棋子的总数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com