
科目: 来源: 题型:
【题目】已知一次函数y=kx+b,当x=2时,y=﹣3,当x=1时,y=﹣1.
(1)求一次函数的解析式;
(2)若该一次函数的图形交x轴y轴分别于A、B两点,求△ABO的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是小明家的住房结构平面图(单位:米),他打算把卧室以外的部分都铺上地砖.

(1)若铺地砖的价格为80元/平方米,那么铺地砖需要花多少钱?(用代数式表示)
(2)已知房屋的高为h米,现需要在客厅和卧室的墙壁上贴壁纸,那么需要多少平方米的壁纸(计算时不扣除门,窗所占的面积)?(用代数式表示)
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司为了了解员工每人所创年利润情况,公司从各部抽取部分员工对每年所创利润进行统计,并绘制如图1,图2统计图.
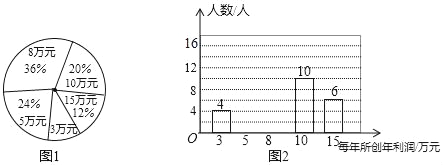
(1)将图2补充完整;
(2)本次共抽取员工 人,每人所创年利润的众数是 万元,平均数是 万元,中位数是 万元;
(3)若每人创造年利润10万元及(含10万元)以上为优秀员工,在公司1200员工中有多少可以评为优秀员工?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,矩形ABCD的两条边在坐标轴上,点D与坐标原点O重合,且AD=8,AB=6.如图2,矩形ABCD沿OB方向以每秒1个单位长度的速度运动,同时点P从A点出发也以每秒1个单位长度的速度沿矩形ABCD的边AB经过点B向点C运动,当点P到达点C时,矩形ABCD和点P同时停止运动,设点P的运动时间为t秒.
(1)当t=5时,请直接写出点D、点P的坐标;
(2)当点P在线段AB或线段BC上运动时,求出△PBD的面积S关于t的函数关系式,并写出相应t的取值范围;
(3)点P在线段AB或线段BC上运动时,作PE⊥x轴,垂足为点E,当△PEO与△BCD相似时,求出相应的t值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,解答下列问题:
,解答下列问题:
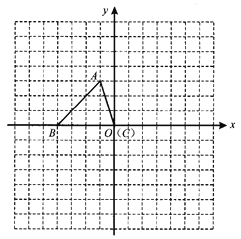
(1)将![]() 向上平移1个单位长度,再向右平移5个单位长度后得到的
向上平移1个单位长度,再向右平移5个单位长度后得到的![]() ,画出
,画出![]() ;
;
(2)![]() 绕原点
绕原点![]() 逆时针方向旋转
逆时针方向旋转![]() 得到
得到![]() ,画出
,画出![]() ;
;
(3)如果利用![]() 旋转可以得到
旋转可以得到![]() ,请直接写出旋转中心
,请直接写出旋转中心![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
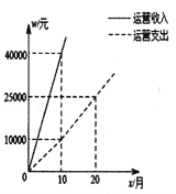
【题目】近年来,共享汽车的出现给人们的出行带来了便利,一辆![]() 型共享汽车的先期成本为8万元,如图是其运营收入
型共享汽车的先期成本为8万元,如图是其运营收入![]() (元)与运营支出
(元)与运营支出![]() (元)关于运营时间
(元)关于运营时间![]() (月)的函数图象.其中
(月)的函数图象.其中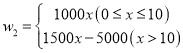 ,一辆
,一辆![]() 型共享汽车的盈利
型共享汽车的盈利![]() (元)关于运营时间
(元)关于运营时间![]() (月)的函数解析式为
(月)的函数解析式为![]()
(1)根据以上信息填空:![]() 与
与![]() 的函数关系式为_________________;
的函数关系式为_________________;
(2)经测试,当![]() ,共享汽车在这个范围内运营相对安全及效益较好,求当
,共享汽车在这个范围内运营相对安全及效益较好,求当![]() ,一辆
,一辆![]() 型共享汽车的盈利
型共享汽车的盈利![]() (元)关于运营时间
(元)关于运营时间![]() (月)的函数关系式;(注:一辆共享汽车的盈利=运营收入-运营支出-先期成本)
(月)的函数关系式;(注:一辆共享汽车的盈利=运营收入-运营支出-先期成本)
(3)某运营公司有![]() 型,
型,![]() 型两种共享汽车,请分析一辆
型两种共享汽车,请分析一辆![]() 型和一辆
型和一辆![]() 型汽车哪个盈利高;
型汽车哪个盈利高;
查看答案和解析>>
科目: 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目: 来源: 题型:
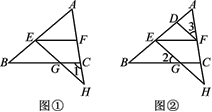
【题目】如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形OABC的边长为2,顶点A,C分别在x轴,y轴的正半轴上,点E是BC的中点,F是AB延长线上一点且FB=1.

(1)求经过点O,A,E三点的抛物线解析式;
(2)点P在抛物线上运动,当点P运动到什么位置时△OAP的面积为2,请求出点P的坐标;
(3)在抛物线上是否存在一点Q,使△AFQ是等腰直角三角形?若存在直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com