
科目: 来源: 题型:
【题目】为了鼓励市民节约用水,某市水费实行分段计费制,每户每月用水量在规定用量及以下的部分收费标准相同,超出规定用量的部分收费标准相同.下表是小明家1至4月份水量和缴纳水费情况,根据表格提供的数据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 7 | 9 | 12 | 15 |
水费(元) | 14 | 18 | 26 | 35 |
(1)规定用量内的收费标准是 元/吨,超过部分的收费标准是 元/吨;
(2)问该市每户每月用水规定量是多少吨?
(3)若小明家六月份应缴水费50元,则六月份他们家的用水量是多少吨?
查看答案和解析>>
科目: 来源: 题型:
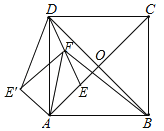
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF、BF、E′F.若AE=2![]() .则四边形ABFE′的面积是_____.
.则四边形ABFE′的面积是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,先将正方形纸片儿对折,折痕为MN,再把点B折叠在折痕MN上,折痕为AE,点E在CB上,点B在MN上的对应点为H,沿AH和DH剪下得到三角形ADH,则下列选项错误的是( )
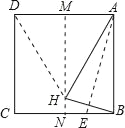
A. DH=AD B. AH=DH C. NE=BE D. DM=![]() DH
DH
查看答案和解析>>
科目: 来源: 题型:
【题目】作图题:如图,在平面内有不共线的3个点,![]() ,
,![]() ,
,![]() .
.
(1)作射线![]() ,在
,在![]() 延长线上取一点
延长线上取一点![]() ,使
,使![]() ;
;
(2)作线段![]() 并延长
并延长![]() 到点
到点![]() ,使
,使![]() ;
;
(3)连接![]() ,
,![]() ;
;
(4)度量线段![]() 和
和![]() 的长度,直接写出二者之间的数量关系,观察
的长度,直接写出二者之间的数量关系,观察![]() 和
和![]() 的位置是(填“平行”或“相交”)关系;
的位置是(填“平行”或“相交”)关系;
(5)作![]() 的中点
的中点![]() ,连接
,连接![]() ,猜想
,猜想![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”)
”)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,C点表示数c,且a、c满足|a+3|+(c﹣9)2=0.若点A与点B之间的距离表示为AB=|a﹣b|,点B与点C之间的距离表示为BC=|b﹣c|,点B在点A、C之间,且满足BC=2AB.
(1)a= ,b= ,c= ;
(2)若点P为数轴上一动点,其对应的数为x,当代数式|x﹣a|+|x﹣b|+|x﹣c|取得最小值时,此时x= ,最小值为 .
(3)动点M从A点位置出发,沿数轴以每秒1个单位的速度向终点C运动,设运动时间为t秒,当点M运动到B点时,点N从A点出发,以每秒2个单位的速度沿数轴向C点运动,N点到达C点后,再立即以同样的速度返回,运动到终点A.问:在点N开始运动后,M、N两点之间的距离能否为2个单位?如果能,请求出运动的时间t的值以及此时对应的M点所表示的数:如果不能,请说明理由.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉你原因和方法.
阅读下列材料:
问题:利用一元一次方程将0.![]() 化成分数.
化成分数.
解:设0.![]() =x.
=x.
方程两边都乘以10,可得10×0.![]() =10x
=10x
由0.![]() =0.777…,可知10×0.
=0.777…,可知10×0. ![]() =7.777…=7+0.
=7.777…=7+0.![]()
即7+x=10x.(请你体会将方程两边都乘以10起到的作用)
可解得x=![]() ,即0.
,即0.![]() =
=![]() .
.
(1)填空:将0.![]() 写成分数形式为 .
写成分数形式为 .
(2)请你仿照上述方法把下列两个小数化成分数,要求写出利用一元一次方程进行解答的过程:①0.![]() ,②0.43
,②0.43![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F.
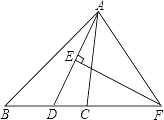
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
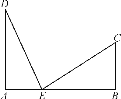
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求直线![]() 的解析式;
的解析式;
(2)设点![]() 为直线
为直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 、
、![]() ,当
,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,直线![]() 过直线
过直线![]() 与
与![]() 轴的交点
轴的交点![]() .设
.设![]() 的中点为
的中点为![]() ,
,![]() 是直线
是直线![]() 上一点,
上一点,![]() 是直线
是直线![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目: 来源: 题型:
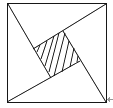
【题目】在北京召开的国际数学家大会会标,它是有四个全等的小正方形拼成的一个大正方形(如图所示),若大正方形的面积为13,小正方形的面积是1,较长的直角边为a,较短的直角边为b,则(a+b)2的值为( )
A.13B.19C.25D.169
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com