
科目: 来源: 题型:
【题目】已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() G为线段
G为线段![]() 上一点,
上一点,![]() 两点分别从
两点分别从![]() 点沿
点沿![]() 方向同时运动,设
方向同时运动,设![]() 点的运动速度为
点的运动速度为![]() 点的运动速度为
点的运动速度为![]() ,运动时间为
,运动时间为![]() .
.
(1)![]() 点对应的数为 ,
点对应的数为 ,![]() 点对应的数为 ;
点对应的数为 ;
(2)若![]() ,试求
,试求![]() 为多少
为多少![]() 时,
时,![]() 两点的距离为
两点的距离为![]() ;
;
(3)若![]() ,点
,点![]() 为数轴上任意一点,且
为数轴上任意一点,且![]() ,请直接写出
,请直接写出![]() 的值.
的值.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我们在“堆石子”游戏中发现:像图(1)中的![]() 这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的
这些数据能够表示成正方形,可将其称为正方形数;类似地,像图(2)中的![]() 这些数据能够表示成三角形,可将其称为三角形数.
这些数据能够表示成三角形,可将其称为三角形数.

(1)第![]() 个正方形数是 ;第
个正方形数是 ;第![]() 个正方形数是 ;
个正方形数是 ;
(2)第![]() 个三角形数是 ;第
个三角形数是 ;第![]() 个三角形数是 ;
个三角形数是 ;
(3)若将一堆小石子按一定规律摆成下列图形,请求出第![]() 个图形中“●”的个数.
个图形中“●”的个数.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B的中心对称得C2,C2与x轴交于另一点C,将C2关于点C的中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_____.
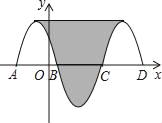
【答案】32
【解析】试题分析:∵抛物线y=﹣x2﹣2x+3与x轴交于点A、B,
∴当y=0时,则﹣x2﹣2x+3=0,
解得x=﹣3或x=1,
则A,B的坐标分别为(﹣3,0),(1,0),
AB的长度为4,
从C1,C3两个部分顶点分别向下作垂线交x轴于E、F两点.
根据中心对称的性质,x轴下方部分可以沿对称轴平均分成两部分补到C1与C2.
如图所示,阴影部分转化为矩形.
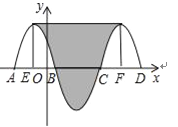
根据对称性,可得BE=CF=4÷2=2,则EF=8
利用配方法可得y=﹣x2﹣2x﹣3=﹣(x+1)2+4
则顶点坐标为(﹣1,4),即阴影部分的高为4,
S阴=8×4=32.
考点:抛物线与x轴的交点.
【题型】填空题
【结束】
17
【题目】解方程:(1)2(3x﹣1)=16;(2)![]() ;(3)
;(3)![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1关于点B中心对称得C2,C2与x轴交于另一点C,将C2关于点C中心对称得C3,连接C1与C3的顶点,则图中阴影部分的面积为_________.
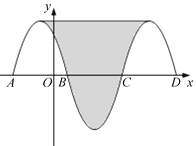
查看答案和解析>>
科目: 来源: 题型:
【题目】元旦期间,丹东新一百商城销售![]() 两种商品,
两种商品,![]() 种商品每件进价
种商品每件进价![]() 元,售价
元,售价![]() 元;
元;![]() 种商品每件售价
种商品每件售价![]() 元,利润率为
元,利润率为![]() .
.
(1)每件![]() 种商品利润率为 ,
种商品利润率为 ,![]() 种商品每件进价为 元;
种商品每件进价为 元;
(2)由于热销,商城决定再购进上面的两种商品共![]() 件(每件商品的进价不变),采购部预算共支出
件(每件商品的进价不变),采购部预算共支出![]() 元,财务部算了一下,说:“如果你用这些钱买两种商品,那么账肯定算错了!”请你用学过的方程知识解释财务部为什么会这样说?
元,财务部算了一下,说:“如果你用这些钱买两种商品,那么账肯定算错了!”请你用学过的方程知识解释财务部为什么会这样说?
查看答案和解析>>
科目: 来源: 题型:
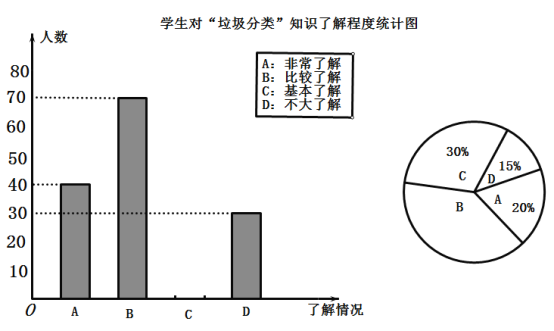
【题目】![]() 年
年![]() 月
月![]() 日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:
日,我市在政府广场举行垃圾分类启动仪式,引导市民正确分类投放垃圾,提高大家环保意识,倡导文明习惯,为调查学生对“垃圾分类”知识的了解程度,玲玲所在的课外小组对本校同学进行了一次随机问卷调查,并将统计的结果绘制了两幅不完整的统计图,请根据图中的信息解答下列问题:
(1)本次调查共调查了 人,“比较了解”所占扇形统计图圆心角的度数为 ;
(2)请将两个统计图补充完整;
(3)若玲玲所在的学校有![]() 人,请你估计一下“非常了解”和“比较了解”大约共有多少人?
人,请你估计一下“非常了解”和“比较了解”大约共有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO![]() ;⑤S△AOC+S△AOB=
;⑤S△AOC+S△AOB=![]() .其中正确的结论是( )
.其中正确的结论是( )
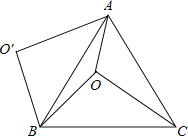
A.①②③⑤B.①②③④C.①②③④⑤D.①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A'B'C'.若∠A=40°,∠B'=110°,∠BCA'的度数是( )
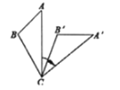
A.110°B.80°C.40°D.30°
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,结合图象回答下列问题:
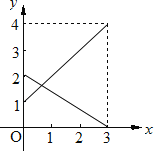
(1)分别求出甲、乙两个蓄水池中水的深度y与注水时间x之间的函数关系式;
(2)求注水多长时间甲、乙两个蓄水池水的深度相同;
(3)求注水多长时间甲、乙两个蓄水池的蓄水量相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com