
科目: 来源: 题型:
【题目】(建立概念)如下图,A、B为数轴上不重合的两定点,点P也在该数轴上,我们比较线段![]() 和
和![]() 的长度,将较短线段的长度定义为点P到线段
的长度,将较短线段的长度定义为点P到线段![]() 的“靠近距离”.特别地,若线段
的“靠近距离”.特别地,若线段![]() 和
和![]() 的长度相等,则将线段
的长度相等,则将线段![]() 或
或![]() 的长度定义为点P到线段
的长度定义为点P到线段![]() 的“靠近距离”.
的“靠近距离”.
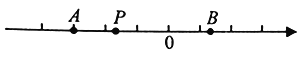
(概念理解)如下图,数轴的原点为O,点A表示的数为![]() ,点B表示的数为4.
,点B表示的数为4.
(1)点O到线段![]() 的“靠近距离”为________;
的“靠近距离”为________;
(2)点P表示的数为m,若点P到线段![]() 的“靠近距离”为3,则m的值为_________;
的“靠近距离”为3,则m的值为_________;

(拓展应用)(3)如下图,在数轴上,点P表示的数为![]() ,点A表示的数为
,点A表示的数为![]() ,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为
,点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为![]() 秒,当点P到线段
秒,当点P到线段![]() 的“靠近距离”为3时,求t的值.
的“靠近距离”为3时,求t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】分别观察下面的左、右两组等式:


根据你发现的规律解决下列问题:
(1)填空:________![]() ;
;
(2)已知![]() ,则x的值是________;
,则x的值是________;
(3)设满足上面特征的等式最左边的数为y,求y的最大值,并写出此时的等式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O是直线![]() 上一点,
上一点,![]() 是一条射线,
是一条射线,![]() 平分
平分![]() ,
,![]() 在
在![]() 内,
内,![]() .
.
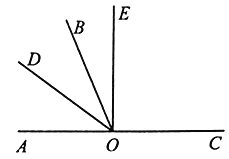
(1)若![]() ,垂足为O点,则
,垂足为O点,则![]() 的度数为________°,
的度数为________°,![]() 的度数为________°;在图中,与
的度数为________°;在图中,与![]() 相等的角有_________;
相等的角有_________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,是由8块棱长都为1的小正方体组合成的简单几何体.

(1)请画出这个几何体的三视图并用阴影表示出来;
(2)该几何体的表面积(含下底面)为________.



查看答案和解析>>
科目: 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为![]() ;②当n为偶数时,结果为
;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数).“C运算”不停地重复进行,例如,
为奇数的正整数).“C运算”不停地重复进行,例如,![]() 时,其“C运算”如下:
时,其“C运算”如下:![]() …若
…若![]() ,则第2020次“C运算”的结果是________.
,则第2020次“C运算”的结果是________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,表中给出的是某月的月历,任意选取“H”型框中的7个数(如阴影部分所示),请你运用所学的数学知识来研究,发现这7个数的和不可能的是()
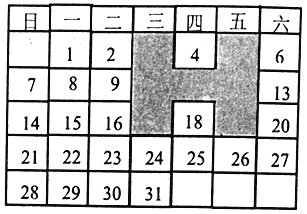
A.63B.70C.92D.105
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注
数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回
袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知线段AB=m(m为常数),点C为直线AB上一点(不与点A、B重合),点M、N分别在线段BC、AC上,且满足CN=3AN,CM=3BM.
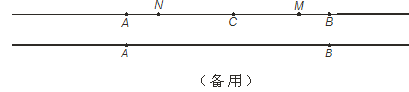
(1)如图,当点C恰好在线段AB中点,且m=8时,则MN=______;
(2) 若点C在点A左侧,同时点M在线段AB上(不与端点重合),请判断CN+2AM -2MN的值是否与m有关?并说明理由.
(3) 若点C是直线AB上一点(不与点A、B重合),同时点M在线段AB上(不与端点重合),求MN长度 (用含m的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,已知直线![]() 与x轴、y轴分别交于A、B两点
与x轴、y轴分别交于A、B两点![]() 直线
直线![]() 直线AB于点
直线AB于点![]() 现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止
现有一点P从点D出发,沿线段DO向点O运动,另一点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到O时,两点都停止![]() 设运动时间为t秒.
设运动时间为t秒.![]() 点A的坐标为______;线段OD的长为______.
点A的坐标为______;线段OD的长为______.![]() 设
设![]() 的面积为S,求S与t之间的函数关系
的面积为S,求S与t之间的函数关系![]() 不要求写出取值范围
不要求写出取值范围![]() ,并确定t为何值时S的值最大?
,并确定t为何值时S的值最大?![]() 是否存在某一时刻t,使得
是否存在某一时刻t,使得![]() 为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.
为等腰三角形?若存在,写出所有满足条件的t的值;若不存在,则说明理由.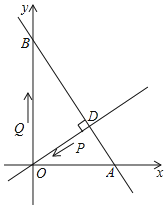
查看答案和解析>>
科目: 来源: 题型:
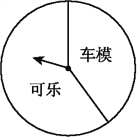
【题目】某商场“六一”期间进行一个有奖销售的活动,设立了一个可以自由转动的转盘(如图),并规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品(若指针落在两个区域的交界处,则重新转动转盘).下表是此次促销活动中的一组统计数据:
转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1 000 |
落在“可乐”区域 的次数m | 60 | 122 | 240 | 298 | 604 | |
落在“可乐” 区域的频率 | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(1)计算并完成上述表格;
(2)请估计当n很大时,频率将会接近__________;假如你去转动该转盘一次,你获得“可乐”的概率约是__________;(结果精确到0.1)
(3)在该转盘中,表示“车模”区域的扇形的圆心角约是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com