
科目: 来源: 题型:
【题目】东坡商贸公司购进某种水果的成本为20元/kg,经市场调研发现,这种水果在未来48天的销售价格p(元/kg)与时间t(天)之间的函数关系式为p=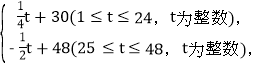 且日销售量y(kg)与销售时间t(天)的关系如下表:
且日销售量y(kg)与销售时间t(天)的关系如下表:

(1)已知y与t的变化规律符合一次函数关系,试求在第30天的日销售量是多少;
(2)问哪一天的销售利润最大,最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,![]() ,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
(2)数轴上,点B关于点A的对称点表示的数是 ;
(3)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2019(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则点M表示的数是 ,点N表示的数是 。
(4)若数轴上P,Q两点间的距离为a(P在Q的左侧),表示数b的点到P,Q的两点的距离相等,将数轴折叠,当P点与Q点重合时,点P表示的数是 ,点Q表示的数是 (用含a,b的式子表示这两个数)。
查看答案和解析>>
科目: 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗. 我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;

查看答案和解析>>
科目: 来源: 题型:
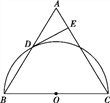
【题目】已知:如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,垂足为点E.
求证:(1)△ABC是等边三角形;(2)AE=![]() CE.
CE.
查看答案和解析>>
科目: 来源: 题型:
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去……
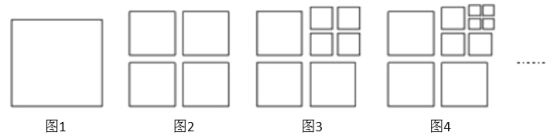
(1)根据图中的规律补全下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
(2)求第几幅图形中有2020个正方形?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数,参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究
问题情境:
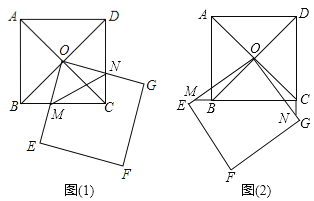
在综合实践课上,李老师让同学们根据如下问题情境,写出两个数学结论:如图(1),正方形ABCD的对角线交于点O,点O又是正方形OEFG的一个顶点(正方形OEFG的边长足够长),将正方形OEFG绕点O做旋转实验,OE与BC交于点M,OG与DC交于点N.
“兴趣小组”写出的两个数学结论是:
①S△OMC+S△ONC=![]() S正方形ABCD;
S正方形ABCD;
②BM2+CM2=2OM2.
问题解决:
(1)请你证明“兴趣小组”所写的两个结论的正确性.
类比探究:
(2)解决完“兴趣小组”的两个问题后,老师让同学们继续探究,再提出新的问题;“智慧小组“提出的问题是:如图(2),将正方形OEFG在图(1)的基础上旋转一定的角度,当OE与CB的延长线交于点M,OG与DC的延长线交于点N,则“兴趣小组”所写的两个结论是否仍然成立?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
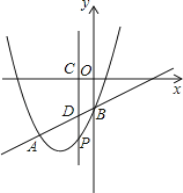
【题目】如图,抛物线y=x2+bx+c与直线y=x﹣1交于A、B两点.点A的横坐标为﹣3,点B在y轴上,点P是y轴左侧抛物线上的一动点,横坐标为m,过点P作PC⊥x轴于C,交直线AB于D.
(1)求抛物线的解析式;
(2)当m为何值时,S四边形OBDC=2S△BPD;
(3)是否存在点P,使△PAD是直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
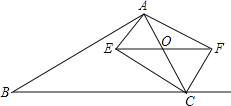
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com