
科目: 来源: 题型:
【题目】![]() 如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
如图4,已知AB为半圆O的直径,BC⊥AB于点B,且BC=AB,D为半圆上一点,连结BD并延长交半圆O的切线AE于点E.
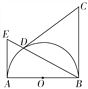
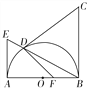
图4① 图4②
(1)如图①,若CD=CB,求证:CD为半圆O的切线;
(2)如图②,若点F在OB上,且FD⊥CD,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() 将一直角三角板的直角顶点放在点
将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的下方.
的下方.
(1)将图1中的三角形板绕点![]() 按照顺时针方向旋转至图2的位置,使得
按照顺时针方向旋转至图2的位置,使得![]() 落在射线
落在射线![]() 上,此时
上,此时![]() 旋转的角度是____°;
旋转的角度是____°;
(2)继续将图2中的三角板绕点![]() 按顺时针方向旋转至图3的位置,使得
按顺时针方向旋转至图3的位置,使得![]() 在
在![]() 的内部,则
的内部,则![]() _____________°;
_____________°;
(3)在上述直角板从图1旋转到图3的位置的过程中,若三角板绕点![]() 按每秒钟
按每秒钟![]() 的速度旋转,当
的速度旋转,当![]() 恰好为
恰好为![]() 的平分线时,此时,三角板绕点
的平分线时,此时,三角板绕点![]() 运动时间为__秒,并说明理由.
运动时间为__秒,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
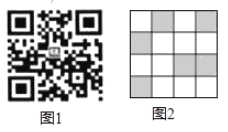
【题目】利用如图1的二维码可以进行身份识别,某校建立了一个身份识别系绕,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为a,b,c,d,那么可以转换为该生所在班级序号,其序号为a×23+b×22+c×21+d×20,如图2第一行数字从左到右依次为0,1,0,1,序号为0×23+1×22+0×21+1×20=5,表示该生为5班学生,那么表示7班学生的识别图案是( )
A.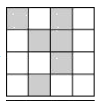 B.
B.
C. D.
D.
查看答案和解析>>
科目: 来源: 题型:
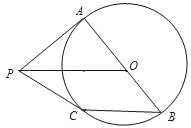
【题目】如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.
(1)判断PC与⊙O的位置关系,并说明理由;
(2)若AB=6,CB=4,求PC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个四位数,记千位上和百位上的数字之和为![]() ,十位上和个位上的数字之和为
,十位上和个位上的数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是 ,最大的“和平数”是 ;
(2)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后的这两个“和平数”为一组“相关和平数”.
例如:1423与4132为一组“相关和平数”
求证:任意的一组“相关和平数”之和是1111的倍数.
(3)求个位上的数字是千位上的数字的两倍且百位上的数字与十位上的数字之和是12的倍数的所有“和平数”;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以线段AB为直径作⊙O,CD与⊙O相切于点E,交AB的延长线于点D, 连接BE,过点O作OC∥BE交切线DE于点C,连接AC .

(1)求证:AC是⊙O的切线 ;
(2)若BD=OB=4,求弦AE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,OB=6cm,OC=8cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】某单位准备组织部分员工到某地旅游,现在联系甲、乙两家旅行社,两家旅行社的报价均为2000元/人,两家旅行社都对10人以上的团体推出优惠条件:甲旅行社对每名员工给予7折优惠;乙旅行社是免去一名员工的费用,其余员工8折优惠.
(1)若该单元参加旅游的员工共有![]() (
(![]() >10)人,请分别表达选择甲、乙旅行社的费用(用含
>10)人,请分别表达选择甲、乙旅行社的费用(用含![]() 的代数式表示并化简).
的代数式表示并化简).
(2)如果参加旅行的员工有20人,分别计算出选择甲、乙旅行社的费用,并判断哪家旅行社收费更便宜.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,PA,PB是⊙O的切线,A,B为切点,点C在PB上,OC∥AP,CD⊥AP于点D.
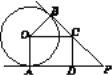
(1)求证:OC=AD;
(2)若∠P=50°,⊙O的半径为4,求四边形AOCD的周长(精确到0.1,参考数据:sin50°≈0.766,cos50°≈0.643,tan50°≈1.192).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com