
科目: 来源: 题型:
【题目】如图,已知平形四边形ABCD中,对角线AC,BD交点O,E是BD延长线上的点,且△ACE是等边三角形.
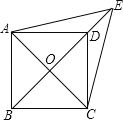
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,AB=2![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目: 来源: 题型:
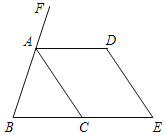
【题目】如图,在下列解答中,填写适当的理由或数学式:
(1)∵AD∥BE,(已知)
∴∠B=∠. ( )
(2)∵∠E+∠ =180°,(已知)
∴AC∥DE. ( )
(3)∵ ∥ ,(已知)
∴∠ACB=∠DAC. ( )
查看答案和解析>>
科目: 来源: 题型:
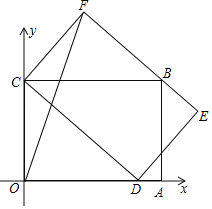
【题目】如图,矩形OABC的边OC在y轴上,边OA在x轴上,C点坐标为(0,3),点D是线段OA的一个动点,连接CD,以CD为边作矩形CDEF,使边EF过点B,已知所作矩形CDEF的面积为12,连接OF,则在点D的运动过程中,线段OF的最大值为__.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,公交车行驶在笔直的公路上,这条路上有![]() ,
,![]() ,
,![]() ,
,![]() 四个站点,每相邻两站之间的距离为5千米,从
四个站点,每相邻两站之间的距离为5千米,从![]() 站开往
站开往![]() 站的车称为上行车,从
站的车称为上行车,从![]() 站开往
站开往![]() 站的车称为下行车.第一班上行车、下行车分别从
站的车称为下行车.第一班上行车、下行车分别从![]() 站、
站、![]() 站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在
站同时发车,相向而行,且以后上行车、下行车每隔10分钟分别在![]() ,
,![]() 站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.
站同时发一班车,乘客只能到站点上、下车(上、下车的时间忽略不计),上行车、下行车的速度均为30千米/小时.

(1)问第一班上行车到![]() 站、第一班下行车到
站、第一班下行车到![]() 站分别用时多少?
站分别用时多少?
(2)若第一班上行车行驶时间为![]() 小时,第一班上行车与第一班下行车之间的距离为
小时,第一班上行车与第一班下行车之间的距离为![]() 千米,求
千米,求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)一乘客前往![]() 站办事,他在
站办事,他在![]() ,
,![]() 两站间的
两站间的![]() 处(不含
处(不含![]() ,
,![]() 站),刚好遇到上行车,
站),刚好遇到上行车,![]() 千米,此时,接到通知,必须在35分钟内赶到,他可选择走到
千米,此时,接到通知,必须在35分钟内赶到,他可选择走到![]() 站或走到
站或走到![]() 站乘下行车前往
站乘下行车前往![]() 站.若乘客的步行速度是5千米/小时,求
站.若乘客的步行速度是5千米/小时,求![]() 满足的条件.
满足的条件.
查看答案和解析>>
科目: 来源: 题型:
【题目】小敏思考解决如下问题:
原题:如图1,点![]() ,
,![]() 分别在菱形
分别在菱形![]() 的边
的边![]() ,
,![]() 上,
上,![]() ,求证:
,求证:![]() .
.
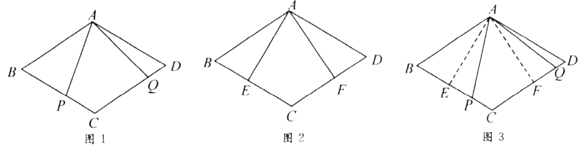
(1)小敏进行探索,若将点![]() ,
,![]() 的位置特殊化:把
的位置特殊化:把![]() 绕点
绕点![]() 旋转得到
旋转得到![]() ,使
,使![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,如图2,此时她证明了
上,如图2,此时她证明了![]() .请你证明.
.请你证明.
(2)受以上(1)的启发,在原题中,添加辅助线:如图3,作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .请你继续完成原题的证明.
.请你继续完成原题的证明.
(3)如果在原题中添加条件:![]() ,
,![]() ,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
,如图1.请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).
查看答案和解析>>
科目: 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
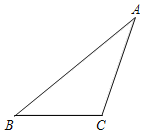
【题目】如图10,在三角形ABC中,∠ACB>90°.
(1)按下列要求画出相应的图形.
①延长BC至点D,使BD=2BC,连接AD;
②过点A画直线BC的垂线,垂足为点E;
③过点C画CG∥AB,CG与AE交于点F,与AD交于点G;
(2)在(1)所画出的图形中,按要求完成下列问题.
①点A、D之间的距离是线段_____的长;点A到线段BC所在的直线的距离是线段___的长,约等于____mm(精确到1mm);
②试说明∠ACD=∠B+∠BAC.
查看答案和解析>>
科目: 来源: 题型:
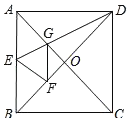
【题目】如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后,折痕DF分别交AB、AC于点E、G,连解FG,下列结论:(1)∠AGD=112.5°;(2)E为AB中点;(3)S△AGD=S△OCD;(4)正边形AEFG是菱形;(5)BE=2OG,其中正确结论的个是( )
A.2B.3C.4D.5
查看答案和解析>>
科目: 来源: 题型:
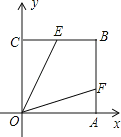
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() .若∠EOF=45°,则F点的纵坐标是( )
.若∠EOF=45°,则F点的纵坐标是( )
A.1B.![]() C.
C.![]() D.
D.![]() ﹣1
﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com