
科目: 来源: 题型:
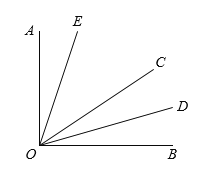
【题目】如图,∠AOC与∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度数.
(2)若∠DOE=54°,求∠EOC的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数![]() 的图象分别交
的图象分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() 两点,点
两点,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒2个单位长度向点
方向以每秒2个单位长度向点![]() 匀速运动,当其中一点到达终点时,另一点也停止运动,设运动时间为
匀速运动,当其中一点到达终点时,另一点也停止运动,设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴,连接
轴,连接![]() 、
、![]() .
.
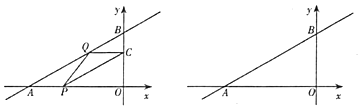
(1)点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
能够成为菱形吗?如果能,求出相应的值;如果不能,说明理由.
(3)若点![]() ,点
,点![]() 在
在![]() 轴上,直线
轴上,直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出
为顶点的四边形是平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,说明理由.
点的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意两点M(x1,y1),N(x2,y2),给出如下定义:
将|x1﹣x2|称为点M,N之间的“横长”,|y1﹣y2|称为点M,N之间的纵长”,点M与点N的“横长”与“纵长”之和称为“折线距离”,记作d(M,N)=|x1﹣x2|+|y1﹣y2|“.
例如:若点M(﹣1,1),点N(2,﹣2),则点M与点N的“折线距离”为:d(M,N)=|﹣1﹣2|+|1﹣(﹣2)|=3+3=6.
根据以上定义,解决下列问题:
已知点P(3,2).
(1)若点A(a,2),且d(P,A)=5,求a的值;
(2)已知点B(b,b),且d(P,B)<3,直接写出b的取值范围;
(3)若第一象限内的点T与点P的“横长”与“纵长”相等,且d(P,T)>5,简要分析点T的横坐标t的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】请仔细阅读下面两则材料,然后解决问题:
材料1:小学时我们学过,任何一个假分数都可以化为一个整数与一个真分数的和的形式,同样道理,任何一个分子次数不低于分母次数的分式都可以化为一个整式与另一个分式的和(或差)的形式,其中分式的分子次数低于分母次数.
如:![]() .
.
材料2:对于式子![]() ,利用换元法,令
,利用换元法,令![]() ,
,![]() .则由于
.则由于![]() ,所以反比例函数
,所以反比例函数![]() 有最大值,且为3.因此分式
有最大值,且为3.因此分式![]() 的最大值为5.
的最大值为5.
根据上述材料,解决下列问题:
(1)把分式![]() 化为一个整式与另一个分式的和的形式,其中分式的分子次数低于分母次数.
化为一个整式与另一个分式的和的形式,其中分式的分子次数低于分母次数.
(2)当![]() 的值变化时,求分式
的值变化时,求分式![]() 的最大(或最小)值.
的最大(或最小)值.
查看答案和解析>>
科目: 来源: 题型:
【题目】购物广场内甲、乙两家商店对A、B两种商品均有优惠促销活动;
甲商店的促销方案是:A商品打八折,B商品打七五折;
乙商店的促销方案是:购买一件A商品,赠送一件B商品,多买多送。
请你结合小明和小华的对话,解答下列问题:
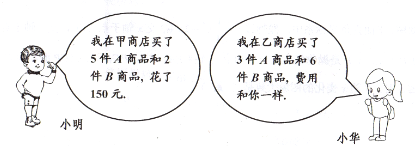
(1)求A、B两种商品促销前的单价;
(2)假设在同一家商店购买A、B两种商品共100件,且A不超过50件,请说明选择哪家商店购买更合算。
查看答案和解析>>
科目: 来源: 题型:
【题目】为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
查看答案和解析>>
科目: 来源: 题型:
【题目】为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。
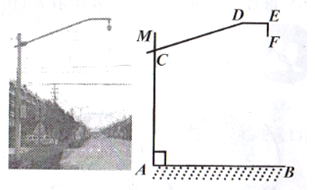
(1)求∠MCD的度数;
(2)求摄像头下端点F到地面AB的距离。(精确到百分位)
(参考数据;sin72°=0.95,cos72°≈0.31,tan72°=3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目: 来源: 题型:
【题目】为深化课改,落实立德树人目标,某学校设置了以下四门拓展性课程:A.数学思维,B.文学鉴赏,C.红船课程,D.3D打印,规定每位学生选报一门.为了解学生的报名情况,随机抽取了部分学生进行调查,并制作成如下两幅不完整的统计图,请回答下列问题:
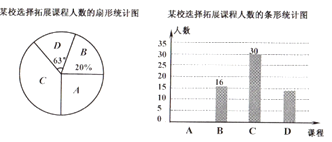
(1)求这次被调查的学生人数;
(2)请将条形统计图补充完整;
(3)假如全校有学生1000人,请估计选报“红船课程”的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com