
科目: 来源: 题型:
【题目】如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
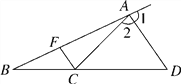
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】规定两数a、b之间的一种运算,记作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(-2,4)= ,(-2,-8)= ;
(2)小明在研究这种运算时发现一个现象:![]() ,他给出了如下的证明:
,他给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]()
∴![]() ,即
,即![]() ,
,
∴![]() .
.
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD中,E.F.G.H依次是各边的中点,O是四边形ABCD内一点,若四边形AEOH.四边形BFOE.四边形CGOF的面积分别为10.12.14,则四边形DHOG的面积=______.
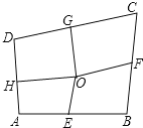
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是伟大的数学家欧拉亲自编的一道题:父亲临终时立下遗嘱,按下述方式分配遗产,老大分得100克朗和剩下的十分之一,老二分得200克朗和剩下的十分之一,老三分得300克朗和剩下的十分之一,老四分得400克朗和剩下的十分之一,… …,依次类推分给其余的孩子,最后发现遗产全部分完后所有孩子分得的遗产相等,遗产总数、孩子人数和每个孩子分得的遗产各是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
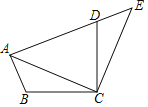
A. 55° B. 60° C. 65° D. 70°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.
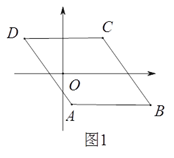
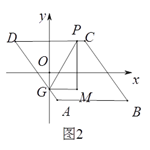
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目: 来源: 题型:
【题目】宁远县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉,B:了解较多,C:一般了解.图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;

查看答案和解析>>
科目: 来源: 题型:
【题目】老师在黑板上出了一道解方程的题:4(2x﹣1)=1﹣3(x+2),小明马上举手,要求到黑板上做,他是这样做的:8x﹣4=1﹣3x+6,①
8x﹣3x=1+6﹣4,②
5x=3,③
x=![]() .④
.④
老师说:小明解一元一次方程没有掌握好,因此解题时出现了错误,请你指出他错在哪一步:________(填编号),并说明理由.然后,你自己细心地解这个方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数;
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由.
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
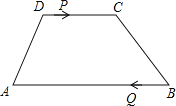
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com