
科目: 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④3a+c=0;则其中说法正确的是( ).

A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,P1、P2是反比例函数y=![]() (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)直接写出反比例函数的解析式.
(2)①求P2的坐标.
②根据图象直接写出在第一象限内,当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y=![]() 的函数值.
的函数值.

查看答案和解析>>
科目: 来源: 题型:
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
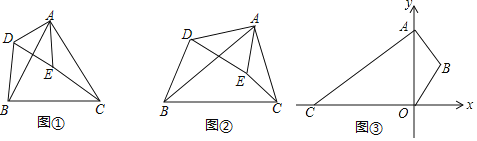
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目: 来源: 题型:
【题目】某班的一次数学小测验中,共有20道选择题,每题答对得相同分数,答错或不答扣相同分数.现从中抽出了四份试卷进行分析,结果如下表:
试卷 | 答对题数 | 答错或不答题数 | 得分 |
A | 17 | 3 | 96 |
B | 14 | 6 | 72 |
C | 18 | 2 | 104 |
D | 20 | 0 | 120 |
(1)此份试卷的满分是多少分?如果全部答错或者不答得多少分?
(2)如果小颖得了0分,那么小颖答对了多少道题?
(3)小慧说她在这次测验中得了60分,她说的对吗?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
3 km | 10 km | -4 km | -3 km | -7 km |
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)该驾驶员离公司距离最远是多少千米?
(3)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
查看答案和解析>>
科目: 来源: 题型:
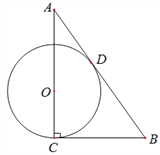
【题目】如图,已知Rt△ABC中,C=90°,O在AC上,以OC为半径作⊙O,切AB于D点,且BC=BD.
(1)求证:AB为⊙O的切线;
(2)若BC=6,sinA=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)的条件下,P点在⊙O上为一动点,求BP的最大值与最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料,并回答下列问题
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;
如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.班里学习小组针对三角形的全等变换进行了探究和讨论
(1)请你写出一种全等变换的方法(除翻折、平移外), .
(2)如图2,前进小组把△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=5,则DC= .
(3)如图3,圆梦小组展开了探索活动,把△ABC纸片沿DE折叠,使点A落在四边形BCDE内部点A′的位置,且得出一个结论:2∠A′=∠1+∠2.请你对这个结论给出证明.
(4)如图4,奋进小组则提出,如果把△ABC纸片沿DE折叠,使点A落在四边形BCDE外部点A′的位置,此时∠A′与∠1、∠2之间结论还成立吗?若成立,请给出证明,若不成立,写出正确结论并证明.

查看答案和解析>>
科目: 来源: 题型:
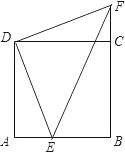
【题目】已知:如图,E点是正方形ABCD的边AB上一点,AB=4,DE=6,△DAE逆时针旋转后能够与△DCF重合.
(1)旋转中心是 .旋转角为 度.
(2)请你判断△DFE的形状,并说明理由.
(3)求四边形DEBF的周长和面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com