
科目: 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目: 来源: 题型:
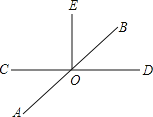
【题目】已知:如图,直线AB、CD相交于点O,EO⊥CD于O.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,请你过点O画直线MN⊥AB,并在直线MN上取一点F(点F与O不重合),然后直接写出∠EOF的度数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在上.
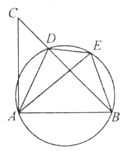
(1)求证:AE=AB;
(2)若∠CAB=90°,cos∠ADB=![]() ,BE=2,求BC的长.
,BE=2,求BC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0) 交x轴正半轴于点A,直线y=2x 经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
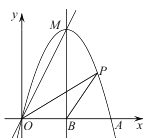
(1)求a,b的值;
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m ,△OBP的面积为S,![]() .求K关于m 的函数表达式及K的范围.
.求K关于m 的函数表达式及K的范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
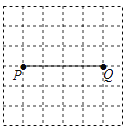
(1)在图1中画出一个面积最小的¨PAQB;
(2)在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,有一个长方体,它的长、宽、高分别为5cm,3cm,4cm.在顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.
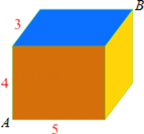
(1)请画出该蚂蚁沿长方体表面爬行的三条线路图(即平面展开图);
(2)已知蚂蚁沿长方体表面爬行的速度是0.8cm/s,问蚂蚁能否在11秒内获取到食物?
查看答案和解析>>
科目: 来源: 题型:
【题目】现有甲、乙、丙等多家食品公司在某市开设蛋糕店,该市蛋糕店数量的扇形统计图如图所示,其中统计图中没有标注相应公司数量的百分比.已知乙公司经营150家蛋糕店,请根据该统计图回答下列问题:
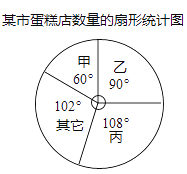
(1)求甲公司经营的蛋糕店数量和该市蛋糕店的总数;
(2)甲公司为了扩大市场占有率,决定在该市增设蛋糕店数量达到全市的20%,求甲公司需要增设的蛋糕店数量.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( ).

A. 2 cm B. 4 cm C. 3 cm D. 5 cm
查看答案和解析>>
科目: 来源: 题型:
【题目】按要求画图,并解答问题
(1)如图,取BC边的中点D,画射线AD;
(2)分别过点B、C画BE⊥AD于点E,CF⊥AD于点F;
(3)BE和CF的位置关系是 ;通过度量猜想BE和CF的数量关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com