
科目: 来源: 题型:
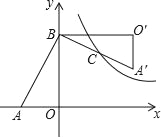
【题目】如图,在Rt△AOB中,直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后,得到△A′O′B,且反比例函数y=![]() 的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
的图象恰好经过斜边A′B的中点C,若SABO=4,tan∠BAO=2,则k=_____.
查看答案和解析>>
科目: 来源: 题型:
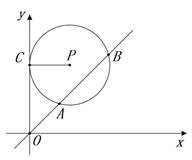
【题目】如图,在平面直角坐标系xOy中,⊙P的圆心是(2,a)(a >0),半径是2,与y轴相切于点C,直线y=x被⊙P截得的弦AB的长为![]() ,则a的值是( )
,则a的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫做角α的余切,记作ctanα,即ctanα=![]() =
=![]() ,根据上述角的余切定义,解下列问题:
,根据上述角的余切定义,解下列问题:
(1)如图1,若BC=3,AB=5,则ctanB= ;
(2)ctan60°= ;
(3)如图2,已知:△ABC中,∠B是锐角,ctan C=2,AB=10,BC=20,试求∠B的余弦cosB的值.

查看答案和解析>>
科目: 来源: 题型:
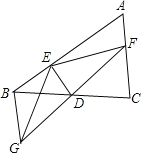
【题目】如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF;
(2)请你判断BE+CF与EF的大小关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知下列命题:①相等的角是对顶角;②互补的角就是平角;③互补的两个角一定是一个锐角,另一个为钝角:④平行于同一条直线的两直线平行;⑤两条平行线被第三条直线所截,同旁内角的角平分线互相垂直.其中,正确命题的个数为( )
A.0B.1个C.2个D.3个
查看答案和解析>>
科目: 来源: 题型:
【题目】点![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() ,
,![]() 两点之间的距离表示为
两点之间的距离表示为![]() ,在数轴上A、B两点之间的距离
,在数轴上A、B两点之间的距离![]() .
.
利用数形结合思想回答下列问题:
(1)数轴上表示-2和1的两点之间的距离是______.
(2)数轴上表示![]() 和-1的两点之间的距离表示为______.
和-1的两点之间的距离表示为______.
(3)在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,且满足
,且满足![]() ,若
,若![]() 是数轴上任意一点,点
是数轴上任意一点,点![]() 表示的数是
表示的数是![]() ,当
,当![]() 时,
时,![]() 的值为多少?
的值为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读材料:用分离系数法进行整式的加减运算.
我们已经学过整式的加减,而我们可以列竖式进行整式的加减运算,只要将参加运算的整式连同字母进行降幂排列,凡缺项则留出空位或添零,然后让常数项对齐(即右对齐)即可.例如,计算(x3﹣2x2﹣5)﹣(x﹣2x2﹣1)时,我们可以用下列竖式计算:
竖式:
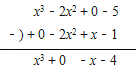
(x3﹣2x2+5)﹣(x﹣2x2﹣1)=x3﹣x﹣4
这种方法叫做分离系数法.用分离系数法计算:
(1)(2x2+4x﹣3)+(5﹣4x+x2);
(2)(3y3﹣5y2﹣6)﹣(y﹣2+3y3).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com