
科目: 来源: 题型:
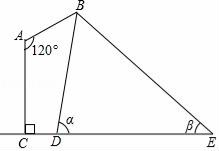
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目: 来源: 题型:
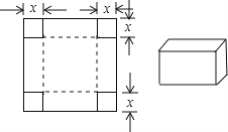
【题目】如图所示,一张边长为16cm的正方形硬纸板,把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为Vcm3,请回答下列问题:
(1)用含有x的代数式表示V,则V=______;
(2)完成下表:
x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
V(cm2) |
(3)观察上表,容积V的值是否随x的增大而增大?当x取什么值时,容积V的值最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,已知AB=8cm,BC=10cm,折叠矩形的一边AD,使点D落在BC边上的点F处,折痕为AE.以点A为原点,分别以AD所在的直线为x轴,AB所在的直线为y轴建立坐标系.
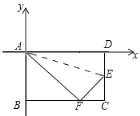
(1)写出点B、D、E、F的坐标;
(2)在坐标轴上是否存在点G,使△AFG是以AF为腰长的等腰三角形?若存在,请求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
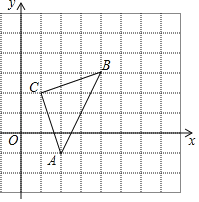
(1)写出点A,B的坐标:A( )、B( );
(2)判断△ABC的形状 ;计算△ABC的面积是 .
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ( ),
( ),![]() ( ),
( ),![]() ( ).
( ).
查看答案和解析>>
科目: 来源: 题型:
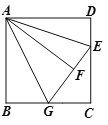
【题目】如图,在正方形ABCD中,AB=3,点E在CD边上,且CE=2DE,将△ADE沿直线AE对折至△AEF,延长EF交BC于G,连接AG,则线段AG的长为______.
查看答案和解析>>
科目: 来源: 题型:
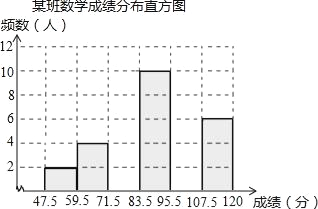
【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成频数分布表如下(成绩得分均为整数):
组别 | 成绩分组 | 频数 | 频率 |
1 | 47.5~59.5 | 2 | 0.05 |
2 | 59.5~71.5 | 4 | 0.10 |
3 | 71.5~83.5 | a | 0.2 |
4 | 83.5~95.5 | 10 | 0.25 |
5 | 95.5~107.5 | b | c |
6 | 107.5~120 | 6 | 0.15 |
合计 | 40 | 1.00 |
根据表中提供的信息解答下列问题:
(1)频数分布表中的a=__________,b=__________,c=__________;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,102018年四川省内江市及以上为优秀,预计优秀的人数约为__________,72分及以上为及格,预计及格的人数约为__________,及格的百分比约为__________;
(3)补充完整频数分布直方图.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了保护环境,某化工厂一期工程完成后购买了3台甲型和2台乙型污水处理设备,共花费资金54万元,且每台乙型设备的价格是每台甲型设备价格的75%.
(1)请你计算每台甲型设备和每台乙型设备的价格各是多少元?
(2)今年该厂二期工程即将完成,产生的污水将大大增加,于是该厂决定再购买甲、乙两种型号设备共8台用于二期工程的污水处理,预算本次购买资金不超过84万元;实际运行中发现,每台甲型设备每月能处理污水200吨,每台乙型设备每月能处理污水160吨,预计二期工程完成后每月将产生不少于1300吨污水,请你求出用于二期工程的污水处理设备的所有购买方案.
(3)经测算:每年用于每台甲型设备的各种维护费和电费为1万元,每年用于每台乙型设备的各种维护费和电费为1.5万元.在(2)中的方案中,哪种购买方案使得设备的各种维护费和电费总费用最低?
查看答案和解析>>
科目: 来源: 题型:
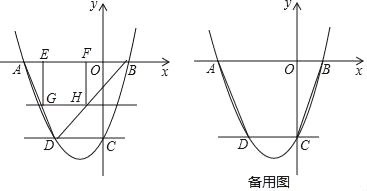
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com