
科目: 来源: 题型:
【题目】小泽和小超分别用掷A、B两枚骰子的方法来确定P(x,y)的位置,她们规定:小泽掷得的点数为x,小超掷得的点数为![]() ,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
,那么,她们各掷一次所确定的点落在已知直线y=-2x+6上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)画出△ABC关于直线L的对称图形.

(2)如图,四边形ABCD是矩形,用直尺和圆规作出∠A的平分线与BC边的垂直平分线的交点Q(不写作法,保留作图痕迹).连结QD,在新图形中,你发现![]() 是_______三角形.
是_______三角形.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线经过原点O(0,0),点A(1,1),点B(![]() ,0).
,0).
(1)求抛物线解析式;
(2)连接OA,过点A作AC⊥OA交抛物线于C,连接OC,求△AOC的面积;
(3)点M是y轴右侧抛物线上一动点,连接OM,过点M作MN⊥OM交x轴于点N.问:是否存在点M,使以点O,M,N为顶点的三角形与(2)中的△AOC相似,若存在,求出点M的坐标;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
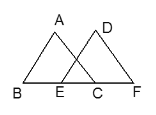
【题目】如图,已知AB∥DE,AB=DE,请你添加一个条件_______ 可以根据“ASA”使得△ABC≌△DEF;或者添加条件BE=CF,可以根据_______得到△ABC≌△DEF。
查看答案和解析>>
科目: 来源: 题型:
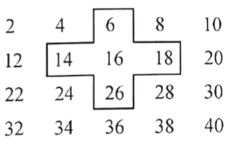
【题目】将连续的偶数2,4,6,8,…,排成如下表,并用一个十字形框架框住其中的五个数,请你仔细观察十字形框架中的数字的规律,并回答下列问题:
(1)十字框中的五个数的和等于 .
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为![]() ,用代数式表示十字框中的五个数的和是 .
,用代数式表示十字框中的五个数的和是 .
(3)在移动十字框的过程中,若框住的五个数的和等于2020,这五个数从小到大依次是: , , , , ,……
(4)框住的五个数的和能等于2019吗?
答: (回答“能”或“不能”)
理由是:_______________________________________________________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:
查看答案和解析>>
科目: 来源: 题型:
【题目】已知下列结论:①若![]() ,则
,则![]() 互为相反数;②若
互为相反数;②若![]() ,则
,则![]() 且
且![]() ;③
;③![]() ;④绝对值小于10的所有整数之和等于0;⑤3与-5是同类项.其中正确的结论有( )个.
;④绝对值小于10的所有整数之和等于0;⑤3与-5是同类项.其中正确的结论有( )个.
A.2B.3C.4D.5
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
已知:如图1,等边△A1A2A3内接于⊙O,点P是![]() 上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:
上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:![]() 是定值.
是定值.
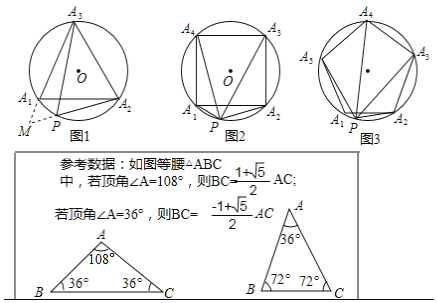
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M

∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
(2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4”,其余条件不变,请问:![]() 还是定值吗?为什么?
还是定值吗?为什么?
(3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则![]() = (只写出结果).
= (只写出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com