
科目: 来源: 题型:
【题目】己知如图,等腰![]() ,
,![]() ,
,![]() ,
,![]() 于点
于点![]() .点
.点![]() 是延长线上一点,点
是延长线上一点,点![]() 是线段上一点,
是线段上一点,![]() 下面的结论: ①
下面的结论: ①![]() ;②
;②![]() ;③
;③![]() 是等边三角形④.
是等边三角形④.![]() 其中正确的是( )
其中正确的是( )
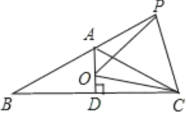
A. ①③④B. ①②③C. ①③D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】有一些相同的房间需要粉刷,一天3名师傅去粉刷8个房间,结果其中有40m2墙面未来得及刷;同样的时间内5名徒弟粉刷了9个房间的墙面。每名师傅比徒弟一天多刷30m2的墙面。
(1)求每个房间需要粉刷的墙面面积;
(2)张老板现有36个这样的房间需要粉刷,若请1名师傅带2名徒弟去,需要几天完成?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有A,B,C,D四张卡片,其正面分别写有“、寸、又、日”,有的能独立成字,有的能组合成字.现四张卡片背面朝上.
(1)任意翻过一张卡片,能独立成字的概率为________;
(2)先任意翻过一张卡片作为左部偏旁,再任意翻过一张与其组合,请用列表或画树状图的方法求翻过的两张卡片恰好能组合成字的概率.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】问题背景:
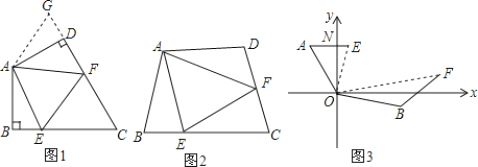
如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠D=90°.E、F分别是BC、CD上的点,且∠EAF=60°.为了探究图中线段BE,EF,FD之间的数量关系,小红的想法是:在EB的延长线上取一点G,使得BG=DF,连接AG,证明△ABG≌△ADF;再证明△AGE≌△AFE,从而得到结论,她的结论是_____________.
探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由.
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西40°的A处,舰艇乙在指挥中心南偏东80°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以50海里/小时的速度,同时舰艇乙沿北偏东50°的方向以70海里/小时的速度各自前进2小时后,在指挥中心观测到甲、乙两舰艇分别到达E,F处,两舰艇与指挥中心之间的夹角为70°,则此时两舰艇之间的距离为______海里.
查看答案和解析>>
科目: 来源: 题型:
【题目】一口袋中装有四根长度分别为1 cm,3 cm,4 cm,5 cm的细木棒,小明手中有一根长度为3 cm的细木棒,现随机从口袋中取出两根细木棒与小明手中的细木棒放在一起,回答下列问题:
(1)求这三根细木棒能构成三角形的概率;
(2)求这三根细木棒能构成直角三角形的概率;
(3)求这三根细木棒能构成等腰三角形的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】公元初,中美洲玛雅人使用的一种数字系统与其他计数方式都不相同,它采用二十进位制但只有3个符号,用点“●”、划“__________”、卵形“![]() ”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
(1)玛雅符号![]() 表示的自然数是__________;
表示的自然数是__________;
(2)请你在右边的方框中画出表示自然数280的玛雅符号:![]()
自然数 | 1 | 2 | 3 | 4 | 5 |
玛雅符号 | ● | ●● | ●●● | ●●●● | _______ |
自然数 | 6 | 7 | 8 | 9 | 10 |
玛雅符号 |
|
|
|
|
|
自然数 | 11 | 12 | … | 15 | 16 |
玛雅符号 |
|
| … |
|
|
自然数 | … | 19 | 20 | … | 100 |
玛雅符号 | … |
|
| … |
|
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD的边长为10厘米,点E在边AB上,且AE=4厘米,如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.设运动时间为t秒.
(1)若点Q的运动速度与点P的运动速度相等,经过2秒后,△BPE与△CQP是否全等?请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,则当t为何值时,能够使△BPE与△CQP全等;此时点Q的运动速度为多少.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com