
科目: 来源: 题型:
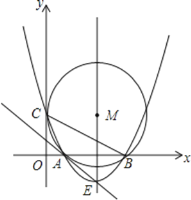
【题目】如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
(1)请直接写出A,B,C三点的坐标,并求出过这三点的抛物线解析式;
(2)设(1)中抛物线解析式的顶点为E,
求证:直线EA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形?
如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图所示放置,使得一直角边重合,连接BD,CE.
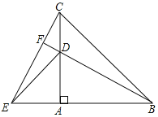
(1)求证:BD=CE;(2)延长BD,交CE于点F,求∠BFC的度数;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点B、E、C、F在一条直线上,AC∥DE,BE=FC,∠A=∠D,
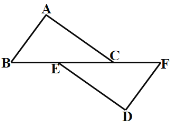
(1) 求证:AB=DF;(2)求证:AB∥DF;(3)若BC=9,EC=5,求BF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。
(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)
(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;
(3)若球一定能越过球网,又不出边界,求h的取值范围。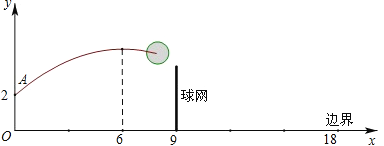
查看答案和解析>>
科目: 来源: 题型:
【题目】“滴滴”司机沈师傅从上午8:00~9:15在东西方向的江平大道上营运,共连续运载十批乘客.若规定向东为正,向西为负,沈师傅营运十批乘客里程如下:(单位:千米)+8,-6,+3,-6,+8,+4,-8,-4,+3,+3.
(1)将最后一批乘客送到目的地时,沈师傅距离第一批乘客出发地的东面还是西面?距离多少千米?
(2) 若汽车每千米耗油0.4升,则8:00~9:15汽车共耗油多少升?
(3)若“滴滴”的收费标准为:起步价8元(不超过3千米),超过3千米,超过部分每千米2元.则沈师傅在上午8:00~9:15一共收入多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算:
(1)![]()
(2)(-36.35)+(-7.25)+26.35+(+7![]() )
)
(3)(﹣99)﹣(+61)﹣(﹣52)+(﹣32)
(4) 49![]() +(-78.21)+27
+(-78.21)+27![]() +(-21.79)
+(-21.79)
(5)![]()
(6)![]()
(7)![]()
(8)![]()
(9) ![]()
(10)![]()
(11) ![]()
(12)![]()
(13)![]() (计算不简便不得分)
(计算不简便不得分)
(14)| —1![]() +(—2
+(—2![]() )| +(—1
)| +(—1![]() )
)
(15)![]()
查看答案和解析>>
科目: 来源: 题型:
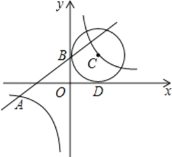
【题目】(题文)如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数
的图象交于点A(﹣4,m),且与y轴交于点B,第一象限内点C在反比例函数![]() 的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
的图象上,且以点C为圆心的圆与x轴,y轴分别相切于点D,B
(1)求m的值;
(2)求一次函数的表达式;
(3)根据图象,当![]() <
<![]() <0时,写出x的取值范围.
<0时,写出x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com