
科目: 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H,则下列结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,CP平分∠ACB,其中正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目: 来源: 题型:
【题目】联想三角形外心的概念,我们可引入如下概念。
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心。
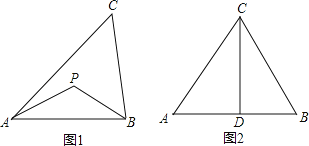
举例:如图1,若PA=PB,则点P为△ABC的准外心。
应用:如图2,CD为等边三角形ABC的高,准外心P在高CD上,且PD=![]() AB,求∠APB的度数。
AB,求∠APB的度数。
探究:已知△ABC为直角三角形,斜边BC=5,AB=3,准外心P在AC边上,试探究PA的长。
查看答案和解析>>
科目: 来源: 题型:
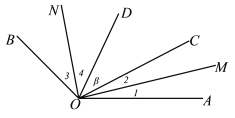
【题目】如图,射线OC、OD在∠AOB内部,∠AOB=![]() ,∠COD=
,∠COD=![]() ,分别作∠AOC和∠BOD的平分线OM、ON,
,分别作∠AOC和∠BOD的平分线OM、ON,
(1)当![]() =130°,
=130°,![]() =40°时,请你填空:∠1+∠3=______°,∠MON=______°;
=40°时,请你填空:∠1+∠3=______°,∠MON=______°;
(2)聪明的小芳通过探究发现,当射线OC、OD的位置在∠AOB内变化时,∠MON与![]() 、
、![]() 之间总满足∠MON=
之间总满足∠MON=![]() ,你是否认同她的这一结论?请说明理由;
,你是否认同她的这一结论?请说明理由;
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC.
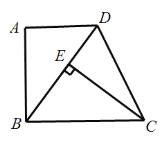
(1)求证:△ABD≌△ECB;
(2)若∠EDC=65°,求∠ECB的度数;
(3)若AD=3,AB=4,求DC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,线段AB=12,动点P从A出发,以每秒2个单位的速度沿射线AB运动,M为AP的中点.
(1)出发多少秒后,PB=2AM?
(2)当P在线段AB上运动时,试说明2BM﹣BP为定值.
(3)当P在AB延长线上运动时,N为BP的中点,下列两个结论:①MN长度不变;②MA+PN的值不变,选择一个正确的结论,并求出其值.
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为 ,线段AD、BE之间的关系 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①请判断∠AEB的度数,并说明理由;②当CM=5时,AC比BE的长度多6时,求AE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列运算及判断正确的是( )
A. ﹣5×![]() ÷(﹣
÷(﹣![]() )×5=1
)×5=1
B. 方程(x2+x﹣1)x+3=1有四个整数解
C. 若a×5673=103,a÷103=b,则a×b=![]()
D. 有序数对(m2+1,m)在平面直角坐标系中对应的点一定在第一象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com