科目： 来源： 题型：
【题目】下列调查方式正确的是（ ）
A.为了解七（1）班同学的课外兴趣爱好情况，采用抽样调查的方式．
B.为了解全区七年级学生对足球的爱好情况，采用抽样调查的方式．
C.为了解新生产的
型药的药效情况，采用全面调查的方式．
D.为了解深圳市民的业余生活情况，采用全面调查的方式．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半，这样的图形有（ ）．
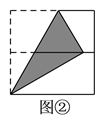
A. 
个 B. 
个 C. 
个 D. 
个
查看答案和解析>>
科目： 来源： 题型：
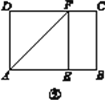
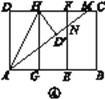
【题目】背景阅读 早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五．它被记载于我国古代著名数学著作《周髀算经》中，在本题中，我们把三边的比为3∶4∶5的三角形称为(3，4，5)型三角形，例如：三边长分别为9，12，15的三角形就是(3，4，5)型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．
实践操作 如图①，在矩形纸片ABCD中，AD＝8 cm，AB＝12 cm.
第一步：如图②，将图①中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．
第二步：如图③，将图②中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF.
第三步：如图④，将图③中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平．
问题解决
(1)请在图②中证明四边形AEFD是正方形；
(2)请在图④中判断NF与ND′的数量关系，并加以证明；
(3)请在图④中证明△AEN是(3，4，5)型三角形．
查看答案和解析>>
科目： 来源： 题型：
【题目】下列说法：①绝对值不大于
的所有整数的和为零，积也为零；②n个有理数相乘，若有奇数个负因数，积必为负数；③
；④如果一个有理数小于1，那么这个数的平方一定小于原数，不正确的有（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目： 来源： 题型：
【题目】已知射线
在
的内部，射线
平分
，射线
平分
．
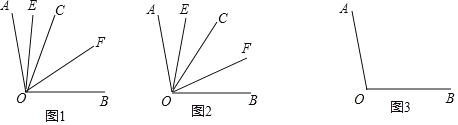
（1）如图1，若
，则
__________度；
（2）若
，
①如图2，若射线在的内部绕点
旋转，求
的度数；
②若射线在的外部绕点旋转（旋转中、
均是指小于180°的角），其余条件不变，请借助图3探究的大小，直接写出的度数．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，已知
和
均为等腰直角三角形，
，点
为
的中点.过点
与
平行的直线交射线
于点
.
（1）当
、
、
三点在同一直线上时（如图1），求证：为
的中点；
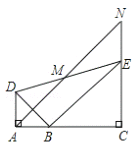
（2）将图1中绕点旋转，当、、三点在同一直线上时（如图2），求证： 
为等腰直角三角形；
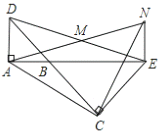
（3）在（2）条件下，已知
，
,求的长.
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，点E是正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．
（1）求证：△ABF≌△CBE；
（2）判断△CEF的形状，并说明理由．
查看答案和解析>>
科目： 来源： 题型：
【题目】如图，△ABC中，∠A＝60°，∠C＝40°，DE垂直平分BC，连接BD．
（1）尺规作图：过点D作AB的垂线，垂足为F．（保留作图痕迹，不写作法）
（2）求证：点D到BA，BC的距离相等．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
