练习册

  • 练习册
  • 试题
    相关习题
     0  357387  357395  357401  357405  357411  357413  357417  357423  357425  357431  357437  357441  357443  357447  357453  357455  357461  357465  357467  357471  357473  357477  357479  357481  357482  357483  357485  357486  357487  357489  357491  357495  357497  357501  357503  357507  357513  357515  357521  357525  357527  357531  357537  357543  357545  357551  357555  357557  357563  357567  357573  357581  366461 

    科目： 来源： 题型：

    【题目】为迎接“七·一”党的生日，某校准备组织师生共310人参加一次大型公益活动，租用4辆大客车和6辆小客车恰好全部坐满，已知每辆大客车的座位数比小客车多15个.

    （1）求每辆大客车和小客车的座位数；

    （2）经学校统计，实际参加活动人数增加了40人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，为使所有参加活动的师生均有座位，最多租用小客车多少辆？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知△ABC是等边三角形，P为△ABC所在平面内一个动点，BP=BA，若0°﹤∠PBC﹤ 180°，且∠PBC的平分线上一点D满足DB=DA.

    (1)当BP和BA重合时(如图1)，则∠BPD=______°.

    (2)当BP在∠ABC内部时(如图2)，求∠BPD的度数

    (3)当BP在∠ABC外部时，请直接写出∠BPD的度数，并画出相应的图形.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】动画片《小猪佩奇》分靡全球，受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片，分别是A佩奇，B乔治，C佩奇妈妈，D佩奇爸爸（四张卡片除字母和内容外，其余完全相同）.姐弟两人做游戏，他们将这四张卡片混在一起，背面朝上放好.

    （1）姐姐从中随机抽取一张卡片，恰好抽到A佩奇的概率为 ；

    （2）若两人分别随机抽取一张卡片（不放回），请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在△ABC中，AB=AC，∠BAC=100°，点D在BC边上，△ABD和△AFD关于直线AD对称，∠FAC的平分线交BC于点G，连接FG．

    (1)求∠DFG的度数.

    (2)设∠BAD=θ，当θ为何值时，△DFG为等腰三角形.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，D、E分别是等边三角形ABC的边AB、AC上的点，且AE=CD，CE、BD交于点P.

    (1)求证：CE=BD.

    (2)求∠BPE的度数.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】为了解同学们每月零花钱数额，校园小记者随机调查了本校部分学生，并根据调查结果绘制出如下不完整的统计图表.

    请根据以上图表，解答下列问题：

    （1）这次被调查的人数共有 人，a= ;

    （2）计算并补全频数分布直方图；

    （3）请估计该校1500名学生中每月零花钱数额低于90元的人数.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中，点D为BC边上一点，∠1＝∠2＝∠3，AC＝AE.

    求证：△ABC≌△ADE；(填空)

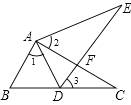
    证明：∵∠2+∠E+∠AFE=180° ( )

    ∠3+∠C+∠CFD=180°(同理)

    又∵∠2＝∠3( )

    ∠AFE=∠CFD( )

    ∴∠E=_________.

    ∵∠1＝∠2(已知)

    ∴∠1+∠CAD＝∠2+∠_______.

    即∠BAC=∠DAE

    在△ABC和△ADE中

    ∴△ABC≌△ADE( ).

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在四边形ABCD中，AD∥BC，∠ABC=90°，AB=BC，E为AB上一点，AE=AD，且BF∥CD，AF⊥CE的延长线于F．连接DE交对角线AC于H．下列结论：①AC垂直平分ED；②AE=BE；③CE=2BF；④BE=2EF.其中结论正确的是_______．(填序号)

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，P为△ABC内的一点，D，E，F分别是点P关于边AB，BC，CA所在直线的对称点，那么∠ADB+∠BEC+∠CFA=______°.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，射线OM在第一象限，且与x轴正半轴的夹角为60°，过点D（6,0)作DA⊥OM于点A，作线段 OD的垂直平分线BE交x轴于点E,交AD于点B,作射线OB.以AB为边在△AOB的外侧作正方形ABCA1,延长A1C交射线OB于点B1,以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2,延长A2C1交射线OB于点B2,以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3……按此规律进行下去，则正方形A2017B2017C2017A2018的周长为______________.

    查看答案和解析>>

    同步练习册答案