
科目: 来源: 题型:
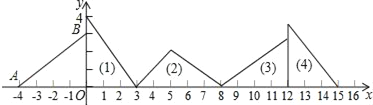
【题目】如图,在平面直角坐标系中,已知点A(﹣4,0)、B(0,3),对△AOB连续作旋转变换依次得到三角形(1)、(2)、(3)、(4)、…,则第(5)个三角形的直角顶点的坐标是_____,第(2018)个三角形的直角顶点的坐标是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD中,点E在AD边上,过点E作AB的平行线,交BC于点F,将矩形ABFE绕着点E逆时针旋转,使点F的对应点落在边CD上,点B的对应点N落在边BC上.
(1)求证:BF=NF;
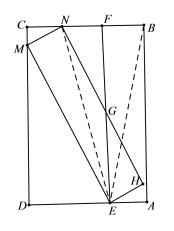
(2)已知AB=2,AE=1,求EG的长;
(3)已知∠MEF=30°,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
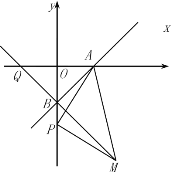
【题目】如图,平面直角坐标系中,点A、B的坐标分别为![]() ,
,![]() ,P为y轴上B点下方一点,
,P为y轴上B点下方一点, ![]() ,以AP为边作等腰直角△APM,其中
,以AP为边作等腰直角△APM,其中![]() ,点M落在第四象限.若直线MB与x轴交于点Q,则Q、M两点中,点_________(填“Q”或“M”)的坐标不随m的变化而变化,该点的坐标为______________.
,点M落在第四象限.若直线MB与x轴交于点Q,则Q、M两点中,点_________(填“Q”或“M”)的坐标不随m的变化而变化,该点的坐标为______________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在学习了第四章《基本的平面图形》的知识后,小明将自己手中的一副三角板的两个直角顶点叠放在一起拼成如下的图形1和图形2.
(1)在图1中,当AD平分∠BAC时,小明认为此时AB也应该平分∠FAD,请你通过计算判断小明的结论是否正确.
(2)小明还发现:只要AD在∠BAC的内部,当△ABC绕直角顶点A旋转时,总有∠FAB=∠DAC(见图2),请你判断小明的发现是否正确,并简述理由.
(3)在图2中,当∠FAC=x,∠BAD=y,请你探究x与y的关系.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),等边△AOC经过平移或轴对称或旋转都可以得到△OBD.
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是 个单位长度;△AOC与△BOD关于直线对称,则对称轴是 ;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是 度.
(2)连接AD,交OC于点E,求AD的长.

查看答案和解析>>
科目: 来源: 题型:
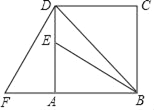
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.
查看答案和解析>>
科目: 来源: 题型:
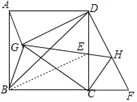
【题目】如图,在边长为2![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是_____.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使得CF=CE,连接BE,DF,将△BEC绕点C按顺时针方向旋转,当点E恰好落在DF上的点H处时,连接AG,DG,BG,则AG的长是_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】两个长为2,宽为1的矩形ABCD和矩形EFGH如图1所示摆放在直线l上,DE=2,将矩形ABCD绕点D顺时针旋转α角(0°<α<90°),将矩形EFGH绕点E逆时针旋转相同的角度.在旋转的过程中,利用图2思考:当矩形ABCD和矩形EFGH重合部分为正方形时,α=_____°.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图放置的两个正方形,大正方形ABCD边长为a,小正方形CEFG边长为b(a>b),M是BC边上一个动点,联结AM,MF,MF交CG于点P,将△ABM绕点A旋转至△ADN,将△MEF绕点F旋转恰好至△NGF.给出以下三个结论:①∠AND=∠MPC; ②△ABM≌△NGF;③S四边形AMFN=a2+b2.
其中正确的结论是_____(请填写序号).

查看答案和解析>>
科目: 来源: 题型:
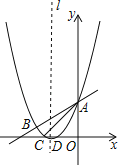
【题目】如图,抛物线y=![]() x2+bx+c与直线y=
x2+bx+c与直线y=![]() x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求抛物线的解析式;
(2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com