[题目]如图.在△ABC中.AB＝BC.∠ABC＝90°.E为BC边上一点(不与B.C重合).D为AB延长线上一点且BD＝BE.点F.G分别为AE.CD的中点.(1)求证:AE＝CD.(2)求证:△B——青夏教育精英家教网—

相关习题

0 357958 357966 357972 357976 357982 357984 357988 357994 357996 358002 358008 358012 358014 358018 358024 358026 358032 358036 358038 358042 358044 358048 358050 358052 358053 358054 358056 358057 358058 358060 358062 358066 358068 358072 358074 358078 358084 358086 358092 358096 358098 358102 358108 358114 358116 358122 358126 358128 358134 358138 358144 358152 366461

科目： 来源： 题型：

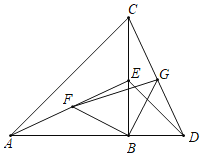
【题目】如图，在△ABC中，AB＝BC，∠ABC＝90°，E为BC边上一点(不与B、C重合)，D为AB延长线上一点且BD＝BE.点F、G分别为AE、CD的中点.

(1)求证：AE＝CD.

(2)求证：△BFG为等腰直角三角形.

查看答案和解析>>

科目： 来源： 题型：

【题目】如图，点E是正方形ABCD的边CD上一点，以A为圆心，AB为半径的弧与BE交于点F，则∠EFD=_____°．

查看答案和解析>>

科目： 来源： 题型：

【题目】一个矩形的长为a，宽为b(a＞0，b＞0)，则矩形的面积为ab.代数式xy(x＞0，y＞0)可以看作是边长为x和y的矩形的面积.我们可以由此解一元二次方程：x2+x﹣6＝0(x＞0).具体过程如下：

①方程变形为x(x+1)＝6.

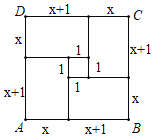
②画四个边长为x+1、x的矩形如图放置；

③由面积关系求解方程.

∵SABCD＝(x+x+1)2，又SABCD＝4x(x+1)+12.

∴(x+x+1)2＝4x(x+1)+1，又x(x+1)＝6，

∴(2x+1)2＝25，

∵x＞0，

∴x＝2.

参照上述方法求关于x的二次方程x2+mx﹣n＝0的解(x＞0，m＞0，n＞0).(要求：画出示意图，标注相关线段的长度，写出解题步骤)

查看答案和解析>>

科目： 来源： 题型：

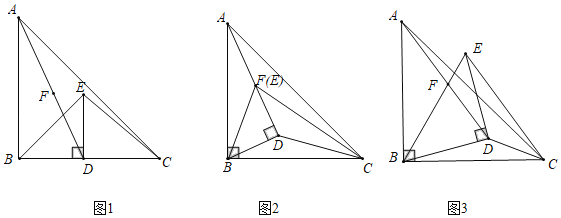
【题目】如图，在△ABC中，∠ABC＝90°，AB＝BC，点D为BC边上任意一点(与B、C不重合)，以BD为直角边构造等腰直角三角形BDE，F为AD的中点.

(1)将△BDE绕点B旋转，当点E与F重合时，求证：∠BAE+∠BCD＝45°.

(2)将△BDE绕点B旋转，当点F在BE上且AB＝AD时，求证：2CD＝BE.

查看答案和解析>>

科目： 来源： 题型：

【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共个，某学习小组做摸球试验，将球搅匀后，从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：

请估计：当很大时，摸到白球的频率将会接近于多少？

摸球的次数
摸到白球的次数
摸到白球的概率

假如你去摸一次，你摸到白球的可能性为多大？这时摸到黑球的可能性为多大？

试估算口袋中黑、白两种颜色的球各有多少个？

查看答案和解析>>

科目： 来源： 题型：

【题目】如图，四边形ABCD中，AD＝2AB，∠ABC＝90°，将△ABC沿BC翻折得到△A′BC，且A′、C、D三点共线，∠A′CB＝52°，则∠CAD＝( )

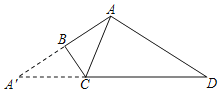
A.78°B.66°C.52°D.38°

查看答案和解析>>

科目： 来源： 题型：

【题目】下列说法一定正确的是( )

A.所有的等边三角形都是全等三角形

B.全等三角形是指形状相同的两个三角形

C.全等三角形是指面积相等的两个三角形

D.全等三角形的周长和面积分别相等

查看答案和解析>>

科目： 来源： 题型：

【题目】问题背景：如图1：在四边形ABCD中,AB=AD,∠BAD=120 ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点。且∠EAF=60° . 探究图中线段BE，EF，FD 之间的数量关系。小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF，可得出结论，他的结论应是_________；

探索延伸：如图2，若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=∠BAD，上述结论是否仍然成立，并说明理由；

实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ，试求此时两舰艇之间的距离。