
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为( )
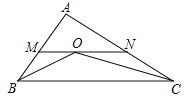
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,高速公路上有A、B两点相距25km,C、D为两村庄,已知DA=10km,CB=15km.DA⊥AB于A,CB⊥AB于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则AE的长是( )km.

A.5B.10C.15D.25
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠BDA=∠CDA,则不一定能使△ABD≌△ACD的条件是( )
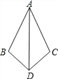
A. BD=DC B. AB=AC C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是半圆
是半圆![]() 的直径,
的直径,![]() 、
、![]() 、
、![]() 是半圆的四等分点,
是半圆的四等分点,![]() 于
于![]() ,连接
,连接![]() 、
、![]() 相交于
相交于![]() 点,连接
点,连接![]() 、
、![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ,其中正确的结论是( )
,其中正确的结论是( )
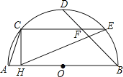
A. ①②③ B. 只有①② C. 只有①③ D. 只有③
查看答案和解析>>
科目: 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:
(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.

【答案】(1)v=![]() (2<t≤5) (2)8米/分
(2<t≤5) (2)8米/分
【解析】分析:(1)由图象可知前一分钟过点(1,2),后三分钟时过点(2,8),分别利用待定系数法可求得函数解析式;
(2)把t=2代入(1)中二次函数解析式即可.
详解:(1)v=at2的图象经过点(1,2),
∴a=2.
∴二次函数的解析式为:v=2t2,(0≤t≤2);
设反比例函数的解析式为v=![]() ,
,
由题意知,图象经过点(2,8),
∴k=16,
∴反比例函数的解析式为v=![]() (2<t≤5);
(2<t≤5);
(2)∵二次函数v=2t2,(0≤t≤2)的图象开口向上,对称轴为y轴,
∴弹珠在轨道上行驶的最大速度在2秒末,为8米/分.
点睛:本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息:自变量的取值范围和图象所经过的点的坐标.
【题型】解答题
【结束】
24
【题目】阅读材料:小胖同学发现这样一个规律:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来则形成一组旋转全等的三角形.小胖把具有这个规律的图形称为“手拉手”图形.如图1,在“手拉手”图形中,小胖发现若∠BAC=∠DAE,AB=AC,AD=AE,则BD=CE.
(1)在图1中证明小胖的发现;
借助小胖同学总结规律,构造“手拉手”图形来解答下面的问题:
(2)如图2,AB=BC,∠ABC=∠BDC=60°,求证:AD+CD=BD;
(3)如图3,在△ABC中,AB=AC,∠BAC=m°,点E为△ABC外一点,点D为BC中点,∠EBC=∠ACF,ED⊥FD,求∠EAF的度数(用含有m的式子表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
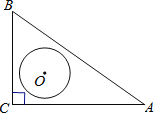
A.r≥1 B.1≤r≤![]() C.1≤r≤
C.1≤r≤![]() D.1≤r≤4
D.1≤r≤4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 厘米,
厘米,![]() 厘米,点
厘米,点![]() 为
为![]() 的中点.如果点
的中点.如果点![]() 在线段
在线段![]() 上以每秒2厘米的速度由
上以每秒2厘米的速度由![]() 点向
点向![]() 点运动,同时,点
点运动,同时,点![]() 在线段
在线段![]() 上以每秒
上以每秒![]() 厘米的速度由
厘米的速度由![]() 点向
点向![]() 点运动,设运动时间为
点运动,设运动时间为![]() (秒)
(秒)![]() .
.

(1)用含![]() 的代数式表示
的代数式表示![]() 的长度;
的长度;
(2)若点![]() 、
、![]() 的运动速度相等,经过1秒后,
的运动速度相等,经过1秒后,![]() 与
与![]() 是否全等,请说明理由;
是否全等,请说明理由;
(3)若点![]() 、
、![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度
的运动速度![]() 为多少时,能够使
为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.

在第![]() 个图形中有______个三角形(用含
个图形中有______个三角形(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com