
科目: 来源: 题型:
【题目】如图,在 4 4 的正方形网格中,有 5 个黑色小正方形.
(1)请你移动一个黑色小正方形,使移动后所形成的4 4 的正方形网格图形是轴对称图形.如:将 8 号小正方形移至 14 号;你的另一种做法是将 号小正方形移至 号(填写标号即可);
(2)请你移动 2 个小正方形,使移动后所形成的图形是轴对称图形.你的一种做法是将 号小正方形移至 号、将 号小正方形移至 号(填写标号即可).

查看答案和解析>>
科目: 来源: 题型:
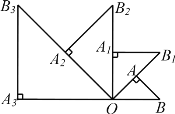
【题目】如图,△ OAB 是腰长为 1 的等腰直角三角形, OAB 90°,延长OA 至 B1 ,使 AB1 OA ,以OB1 为底,在△ OAB 外侧作等腰直角三角形OA1B1 ,再延长OA1 至 B2 , 使 A1B2 OA1 ,以OB2 为底,在△ OA1B1 外侧作等腰直角三角形OA2 B2 ,……,按此规律作等腰直角三角形OAn Bn ( n 1 , n 为正整数),回答下列问题:
(1) A3B3 的长是_____________;(2)△ OA2020 B2020 的面积是_____________.
查看答案和解析>>
科目: 来源: 题型:
【题目】我们把形如x2=a(其中a是常数且a≥0)这样的方程叫做x的完全平方方程.
如x2=9,(3x﹣2)2=25,![]() …都是完全平方方程.
…都是完全平方方程.
那么如何求解完全平方方程呢?
探究思路:
我们可以利用“乘方运算”把二次方程转化为一次方程进行求解.
如:解完全平方方程x2=9的思路是:由(+3)2=9,(﹣3)2=9可得x1=3,x2=﹣3.
解决问题:
(1)解方程:(3x﹣2)2=25.
解题思路:我们只要把 3x﹣2 看成一个整体就可以利用乘方运算进一步求解方程了.
解:根据乘方运算,得3x﹣2=5 或 3x﹣2= .
分别解这两个一元一次方程,得x1=![]() ,x2=﹣1.
,x2=﹣1.
(2)解方程![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点D,直线
轴交于点D,直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 交于点C.
交于点C.
(1)求直线![]() 的解析表达式;
的解析表达式;
(2)求![]() 的面积;
的面积;
(3)在直线![]() 上存在异于点C的另一点P,使得
上存在异于点C的另一点P,使得![]() 与
与![]() 的面积相等,请求出点P的坐标.
的面积相等,请求出点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C,D两点,点E为⊙O上一动点,CF⊥AE于F,则弦AB的长度为________;点E在运动过程中,线段FG的长度的最小值为________.

查看答案和解析>>
科目: 来源: 题型:
【题目】某工厂生产部门为了解本部门工人的生产能力情况,进行了抽样调查.该部门随机抽取了30名工人某天每人加工零件的个数,数据如下:
20 | 21 | 19 | 16 | 27 | 18 | 31 | 29 | 21 | 22 |
25 | 20 | 19 | 22 | 35 | 33 | 19 | 17 | 18 | 29 |
18 | 35 | 22 | 15 | 18 | 18 | 31 | 31 | 19 | 22 |
整理上面数据,得到条形统计图:
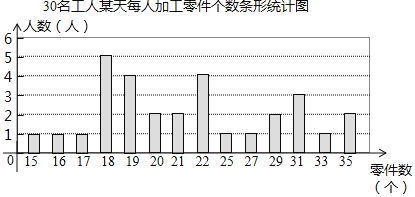
样本数据的平均数、众数、中位数如下表所示:
统计量 | 平均数 | 众数 | 中位数 |
数值 | 23 | m | 21 |
根据以上信息,解答下列问题:
(1)上表中众数m的值为 ;
(2)为调动工人的积极性,该部门根据工人每天加工零件的个数制定了奖励标准,凡达到或超过这个标准的工人将获得奖励.如果想让一半左右的工人能获奖,应根据 来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”)
(3)该部门规定:每天加工零件的个数达到或超过25个的工人为生产能手.若该部门有300名工人,试估计该部门生产能手的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是一次函数
是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
![]() 求直线
求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标及
的坐标及![]() 的面积;
的面积;
![]() 在
在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 的值最大?若存在,直接写出点
的值最大?若存在,直接写出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
![]() 当点
当点![]() 在双曲线上运动时,作以
在双曲线上运动时,作以![]() 、
、![]() 为邻边的平行四边形,求平行四边形周长最小时点
为邻边的平行四边形,求平行四边形周长最小时点![]() 的坐标.
的坐标.

查看答案和解析>>
科目: 来源: 题型:
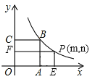
【题目】如图所示,已知正方形![]() 的面积为
的面积为![]() ,点
,点![]() 在函数
在函数![]() 的图象上,点
的图象上,点![]() 是函数
是函数![]() 的图象上动点,过点
的图象上动点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,若设矩形
,若设矩形![]() 和正方形
和正方形![]() 不重合的两部分的面积和为
不重合的两部分的面积和为![]() .
.
![]() 求
求![]() 点坐标和
点坐标和![]() 的值;
的值;
![]() 写出
写出![]() 关于
关于![]() 的函数关系和
的函数关系和![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】己知函数![]() 为反比例函数.
为反比例函数.
己知函数![]() 为反比例函数.
为反比例函数.
![]() 求
求![]() 的值;
的值;
![]() 它的图象在第________象限内,在各象限内,
它的图象在第________象限内,在各象限内,![]() 随
随![]() 增大而________;(填变化情况)
增大而________;(填变化情况)
![]() 当
当![]() 时,此函数的最大值为________,最小值为________.
时,此函数的最大值为________,最小值为________.
查看答案和解析>>
科目: 来源: 题型:
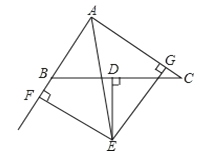
【题目】如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=![]() (AB+AC).
(AB+AC).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com