
科目: 来源: 题型:
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△BCD中,∠CBD=90°,BC=BD,点A在CB的延长线上,且BA=BC,点E在直线BD上移动,过点E作射线EF⊥EA,交CD所在直线于点F.

(1)试求证图(1)中:∠BAE=∠DEF;
(2)当点E在线段BD上移动时,如图(1)所示,求证:AE=EF;
(3)当点E在直线BD上移动时,在图(2)与图(3)中,分别猜想线段AE与EF有怎样的数量关系,并就图(3)的猜想结果说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读并完成下列问题
通过观察,发现方程:x+![]() =2+
=2+![]() 的解是:x1=2,x2=
的解是:x1=2,x2=![]() ;
;
x+![]() =3+
=3+![]() 的解是:x1=3,x2=
的解是:x1=3,x2=![]() ;
;
x+![]() =4+
=4+![]() 的解是:x1=4,x2=
的解是:x1=4,x2=![]() ;
;
……
(1)观察方程的解,猜想关于x的方程x+![]() =10+
=10+![]() 的解是 ;根据以上规律,猜想关于x的方程x+
的解是 ;根据以上规律,猜想关于x的方程x+![]() =m+
=m+![]() 的解是 ;
的解是 ;
(2)利用上述规律解关于x的方程![]() =a+
=a+![]() .
.
查看答案和解析>>
科目: 来源: 题型:
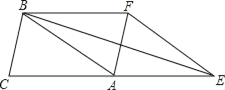
【题目】如图,已知△ABC的面积为3,且AB=AC,现将△ABC沿CA方向平移CA长度得到△EFA.
(1)求四边形CEFB的面积;
(2)试判断AF与BE的位置关系,并说明理由;
(3)若∠BEC=15°,求AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】在等边△ABC中,D是△ABC内一点,且DA=DB,E为△ABC外一点,连接BE交AC于F,BE=BC,BD平分∠EBC,连接DE,CE,AD∥CE.
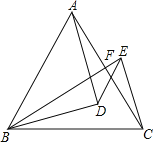
(1)求证:∠DAC=∠DBE;
(2)若AB=6,求△BEC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
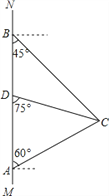
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
(1)抛物线与x轴的另一个交点坐标; ;
(2)方程ax2+bx+c=0的两个根是 ;
(3)不等式ax2+bx+c<0的解是 ;
(4)y随x的增大而减小的自变量x的取值范围是 ;
(5)求出抛物线的解析式及顶点坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】国家统计局网站近日发布一组数据显示,2017年中国创新指数为196.3,比上年增长6.8%,测算结果表明,2017年,中国创新环境进一步优化,创新投入力度继续加大,创新产出持续提升,创新成效稳步增强,创新能力向高质量发展要求稳步迈进.渝北区政府在创新环境建设中,拟对城区部分路段的人行道、绿化带、排水管道等公用设施更新改造.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需20天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)市政府决定由甲、乙共同完成此项工程.若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,若工程总费用不超过143万元,则甲工程队至少工作多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何.”(译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?)若买得公鸡和母鸡之和不超过20只,且买得公鸡数不低于母鸡数,则此时买得小鸡_____只.
查看答案和解析>>
科目: 来源: 题型:
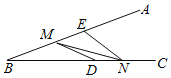
【题目】如图,∠ABC=20°,点D,E分别在射线BC,BA上,且BD=3,BE=3,点M,N分别是射线BA,BC上的动点,求DM+MN+NE的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com