
科目: 来源: 题型:
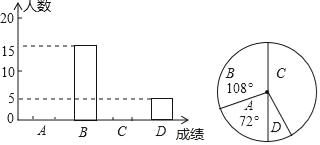
【题目】某校九年级数学测试后,为了解学生学习情况,随机抽取了九年级部分学生的数学成绩进行统计,得到相关的统计图表如下.
成绩/分 | 120﹣111 | 110﹣101 | 100﹣91 | 90以下 |
成绩等级 | A | B | C | D |
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的数学成绩,补全频数分布直方图;
(2)若该校九年级有1000名学生,请据此估计该校九年级此次数学成绩在B等级以上(含B等级)的学生有多少人?
(3)根据学习中存在的问题,通过一段时间的针对性复习与训练,若A等级学生数可提高40%,B等级学生数可提高10%,请估计经过训练后九年级数学成绩在B等级以上(含B等级)的学生可达多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目: 来源: 题型:
【题目】如下图,已知直线![]() 分别与
分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,直线
两点,直线![]() :
:![]() 交
交![]() 于点
于点![]() .
.
(1)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(2)如图1,点E是线段OB的中点,连结AE,点F是射线OG上一点, 当![]() ,且
,且![]() 时,求
时,求![]() 的长;
的长;
(3)如图2,若![]() ,过
,过![]() 点作
点作![]() ∥
∥![]() ,交
,交![]() 轴于点
轴于点![]() ,此时在
,此时在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
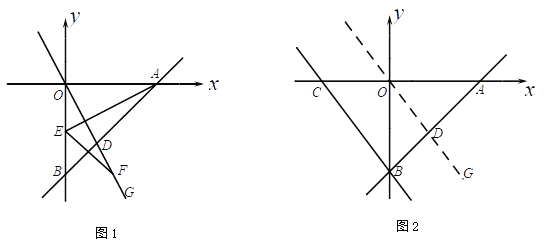
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两车先后从“深圳书城”出发,沿相同的路线到距书城240km的某市.因路况原因,甲车行驶的路程y (km)与甲车行驶的时间x (h)的函数关系图象为折线 O-A-B, 乙车行驶的路程y (km)与甲车行驶的时间x(h)的函数关系图象为线段CD.
(1)求线段AB所在直线的函数表达式;
(2)①乙车比甲车晚出发 小时;
②乙车出发多少小时后追上甲车?
(3)乙车出发多少小时后甲、乙两车相距10千米?

查看答案和解析>>
科目: 来源: 题型:
【题目】已知直角△ABC中,∠C=90°,∠A=30°,AB=4,以AC为腰,在△ABC外作顶角为30°的等腰三角形ACD,连接BD.请画出图形,并直接写出△BCD的面积.
查看答案和解析>>
科目: 来源: 题型:
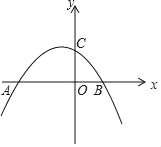
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
x2+bx+c与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C.请解答下列问题:
(1)求抛物线的函数解析式并直接写出顶点M坐标;
(2)连接AM,N是AM的中点,连接BN,求线段BN长.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(﹣![]() ,
,![]() ).
).
查看答案和解析>>
科目: 来源: 题型:
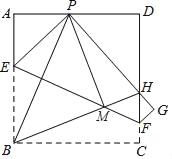
【题目】如图,正方形纸片ABCD,P为正方形AD边上的一点(不与点A,点D重合),将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF,连接BP,BH.BH交EF于点M,连接PM.下列结论:①BE=PE;②EF=BP;③PB平分∠APG;④MH=MF;⑤BP=![]() BM,其中正确结论的个数是( )
BM,其中正确结论的个数是( )
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目: 来源: 题型:
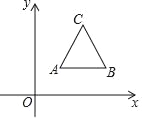
【题目】等边△ABC如图放置,A(1,1),B(3,1),等边三角形的中心是点D,若将点D绕点A旋转90°后得到点D′,则D′的坐标( )
A. (1+![]() ,0) B. (1﹣
,0) B. (1﹣![]() ,0)或(1+
,0)或(1+![]() ,2)
,2)
C. (1+![]() ,0)或(1﹣
,0)或(1﹣![]() ,2) D. (2+
,2) D. (2+![]() ,0)或(2﹣
,0)或(2﹣![]() ,0)
,0)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是两个可以自由转动的由红、蓝两色构成的转盘,其中转盘![]() 的蓝色部分占整个转盘的
的蓝色部分占整个转盘的![]() ,转盘
,转盘![]() 中的蓝色占整个转盘的
中的蓝色占整个转盘的![]() .转动转盘,转盘停止后指针所指颜色就是转出的颜色,现在甲、乙两个人做游戏.
.转动转盘,转盘停止后指针所指颜色就是转出的颜色,现在甲、乙两个人做游戏.
![]() 甲转动转盘
甲转动转盘![]() ,乙转动转盘
,乙转动转盘![]() ,每人转动十次,谁转出的红色次数多谁获胜.你认为这个游戏公平吗?如果不公平,谁容易获胜,请说明理由;
,每人转动十次,谁转出的红色次数多谁获胜.你认为这个游戏公平吗?如果不公平,谁容易获胜,请说明理由;
![]() 小明提出下面的改进方案:由第三个人来转动上面的两个转盘,如果两个转盘都转出了红色,则甲赢,否则乙赢,请你帮小明设计一种替代试验的方法,并写出试验的步骤.
小明提出下面的改进方案:由第三个人来转动上面的两个转盘,如果两个转盘都转出了红色,则甲赢,否则乙赢,请你帮小明设计一种替代试验的方法,并写出试验的步骤.

查看答案和解析>>
科目: 来源: 题型:
【题目】小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了![]() 次实验,实验的结果如下:
次实验,实验的结果如下:
朝上的点数 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 计算“
计算“![]() 点朝上”的频率和“
点朝上”的频率和“![]() 点朝上”的频率.
点朝上”的频率.
![]() 小颖说:“根据实验,一次实验中出现
小颖说:“根据实验,一次实验中出现![]() 点朝上的概率最大”;小红说:“如果投掷
点朝上的概率最大”;小红说:“如果投掷![]() 次,那么出现
次,那么出现![]() 点朝上的次数正好是
点朝上的次数正好是![]() 次.”小颖和小红的说法正确吗?为什么?
次.”小颖和小红的说法正确吗?为什么?
![]() 小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为
小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为![]() 的倍数的概率.
的倍数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com