
科目: 来源: 题型:
【题目】二次函数![]() ,
,![]() ,
,![]() 是常数,且
是常数,且![]() 中的
中的![]() 与
与![]() 的部分对应值如下表所示,则下列结论中,正确的个数有( )
的部分对应值如下表所示,则下列结论中,正确的个数有( )
|
|
|
|
|
|
|
|
|
|
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而减小;
值的增大而减小;
![]() 方程
方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知直线![]() 的同侧有两个点
的同侧有两个点![]() 、
、![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使
,使![]() 点到
点到![]() 、
、![]() 两点的距离之和最短的问题,可以通过轴对称来确定,即作出其中一点关于直线
两点的距离之和最短的问题,可以通过轴对称来确定,即作出其中一点关于直线![]() 的对称点,对称点与另一点的连线与直线
的对称点,对称点与另一点的连线与直线![]() 的交点就是所要找的点,通过这种方法可以求解很多问题.
的交点就是所要找的点,通过这种方法可以求解很多问题.
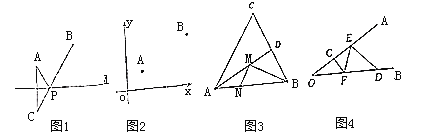
(1)如图2,在平面直角坐标系内,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 在
在![]() 轴上,求
轴上,求![]() 的最小值;
的最小值;
(2)如图3,在锐角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分线交
的角平分线交![]() 于点
于点![]() ,
,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,则
上的动点,则![]() 的最小值为______.
的最小值为______.
(3)如图4,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是射线
分别是射线![]() ,
,![]() 上的动点,则
上的动点,则![]() 的最小值为__________.
的最小值为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() 的图象经过点A(
的图象经过点A(![]() ,
,![]() ),且与正比例函数
),且与正比例函数![]() 的图象交于点B(
的图象交于点B(![]() ,
,![]() ).
).
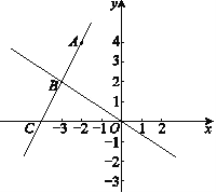
(1)求![]() 的值及一次函数
的值及一次函数![]() 的解析式;
的解析式;
(2)若一次函数![]() 的图象与x轴交于点C,且正比例函数
的图象与x轴交于点C,且正比例函数![]() 的图象向下平移m(m>0)个单
的图象向下平移m(m>0)个单
位长度后经过点C,求m的值;
(3)直接写出关于x的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,已知
,已知![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如图,观察并猜想![]() 和
和![]() 有怎样的数量关系?并说明理由.
有怎样的数量关系?并说明理由.
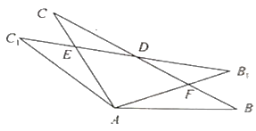
(2)筝形的定义:两组邻边分别相等的四边形叫做筝形. 如上图,证明四边形![]() 是筝形.
是筝形.
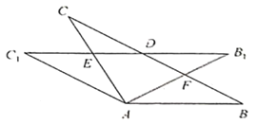
(3)如图,若![]() ,其他条件不变,求
,其他条件不变,求![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,同时也给自行车商家带来商机. 某自行车行销售![]() 型,
型,![]() 型两种自行车,经统计,2019年此车行销售这两种自行车情况如下:
型两种自行车,经统计,2019年此车行销售这两种自行车情况如下:![]() 自行车销售总额为8万元. 每辆
自行车销售总额为8万元. 每辆![]() 型自行车的售价比每辆
型自行车的售价比每辆![]() 型自行车的售价少200元,
型自行车的售价少200元,![]() 型自行车销售数量是
型自行车销售数量是![]() 自行车的1. 25倍,
自行车的1. 25倍, ![]() 自行车销售总额比A型自行车销售总额多
自行车销售总额比A型自行车销售总额多![]() .
.
(1)求每辆![]() 型自行车的售价多少元.
型自行车的售价多少元.
(2)若每辆![]() 型自行车进价1400元,每辆
型自行车进价1400元,每辆![]() 型自行车进价1300元,求此自行车行2019年销售
型自行车进价1300元,求此自行车行2019年销售![]() 型自行车的总利润.
型自行车的总利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并完成任务. 三角形的外心定义:三角形三边的垂直平分线相交于一点,这个点叫做三角形的外心,如图1,直线![]() 分别是边
分别是边![]() 的垂直平分线.
的垂直平分线.
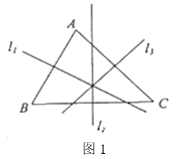
求证:直线![]() 相交于一点.
相交于一点.
证明:如图2,设![]() 相交于点
相交于点![]() ,分别连接
,分别连接![]()
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() ,(依据1)
,(依据1)
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() ,
,
∴![]() ,(依据2)
,(依据2)
∵![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴点![]() 在
在![]() 上,(依据3)
上,(依据3)
∴直线![]() 相交于一点.
相交于一点.
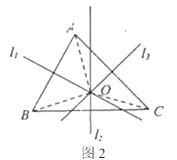
(1)上述证明过程中的“依据1”“依据2”“依据3”分别指什么?
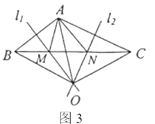
(2)如图3,直线![]() 分别是
分别是![]() 的垂直平分线,直线
的垂直平分线,直线![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 的外心,
的外心,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,分别连接
,分别连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() . 若
. 若![]() ,
,![]() 的周长为
的周长为![]() ,求
,求![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com