
科目: 来源: 题型:
【题目】完成下面的说理过程:如图,在四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 延长线上的点,连接
延长线上的点,连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .已知
.已知![]() ,
,![]() .对
.对![]() 和
和![]() 说明理由.
说明理由.

理由:![]() (已知),
(已知),
![]() (______),
(______),
![]() (等量代换).
(等量代换).
![]() (______).
(______).
![]() (______).
(______).
![]() (______),
(______),
![]() (______).
(______).
![]() (______).
(______).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知张强家、体育场、文具店在同一直线上.如图的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.图中x表示时间,y表示张强离家的距离.则下列说法错误的是( )

A. 体育场离张强家2.5千米
B. 体育场离文具店1千米
C. 张强在文具店逗留了15分钟
D. 张强从文具店回家的平均速度是![]() 千米/分
千米/分
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,设出发的时间为
,设出发的时间为![]() 秒.
秒.

(1)出发2秒后,求![]() 的周长.
的周长.
(2)问![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,若
,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分?
的两部分?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:在平面直角坐标系中,对于任意两点![]() ,
,![]() ,若点
,若点![]() 满足
满足![]() ,
,![]() ,那么称点
,那么称点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
例如:![]() ,
,![]() ,当点
,当点![]() 满是
满是![]() ,
,![]() 时,则点
时,则点![]() 是点
是点![]() ,
,![]() 的融合点,
的融合点,

(1)已知点![]() ,
,![]() ,
,![]() ,请说明其中一个点是另外两个点的融合点.
,请说明其中一个点是另外两个点的融合点.
(2)如图,点![]() ,点
,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是点
是点![]() ,
,![]() 的融合点.
的融合点.
①试确定![]() 与
与![]() 的关系式.
的关系式.
②若直线![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 为直角三角形时,求点
为直角三角形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
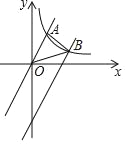
【题目】如图,已知直线y=![]() x与反比例函数y=
x与反比例函数y=![]() (x>0)的图象交于点A(2,m);将直线y=
(x>0)的图象交于点A(2,m);将直线y=![]() x向下平移后与反比例函数y=
x向下平移后与反比例函数y=![]() (x>0)的图象交于点B,且△AOB的面积为3.
(x>0)的图象交于点B,且△AOB的面积为3.
(1)求k的值;
(2)求平移后所得直线的函数表达式.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
(1)求证:PB=QC;
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.
(千米)的函数图象.
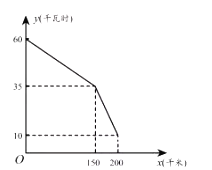
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程,当![]() 时,求1千瓦时的电量汽车能行驶的路程;
时,求1千瓦时的电量汽车能行驶的路程;
(2)当![]() 时求
时求![]() 关于
关于![]() 的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.
查看答案和解析>>
科目: 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目: 来源: 题型:
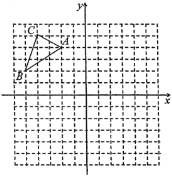
【题目】已知![]() 在平面直角坐标系中的位置如图所示,将
在平面直角坐标系中的位置如图所示,将![]() 向右平移5个单位长度,再向下平移3个单位长度得到
向右平移5个单位长度,再向下平移3个单位长度得到![]() .(图中每个小方格边长均为1个单位长度)
.(图中每个小方格边长均为1个单位长度)
(1)在图中画出平移后的![]() ;
;
(2)直接写出![]() 各顶点的坐标
各顶点的坐标![]() ______,
______,![]() ______,
______,![]() ______.
______.
(3)在![]() 轴上找到一点
轴上找到一点![]() ,当
,当![]() 取最小值时,
取最小值时,![]() 点的坐标是______.
点的坐标是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com