
科目: 来源: 题型:
【题目】某校八年级举行数学趣味竞赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元. 根据比赛设奖情况,需购买两种笔记本共30本,并且购买A笔记本的数量要少于B笔记本数量的![]() ,但又不少于B笔记本数量的
,但又不少于B笔记本数量的![]() .
.
(1)求A笔记本数量的取值范围;
(2)购买这两种笔记本各多少本时,所需费用最省?最省费用是多少元?
查看答案和解析>>
科目: 来源: 题型:
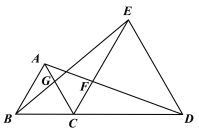
【题目】如图,点C为线段BD上一点,△ABC、△CDE都是等边三角形.AD与CE交于点F,BE与AC相交于点G.
(1)求证:△ACD≌△BCE;
(2)若CF+CG=8,BD=18,求△ACD的面积.
查看答案和解析>>
科目: 来源: 题型:
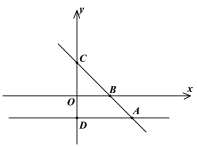
【题目】如图,在平面直角坐标系中,直线y=﹣x+m过点A(5,—2)且分别与x轴、y轴交于点B、C,过点A画AD//x轴,交y轴于点D.
(1)求点B、C的坐标;
(2)在线段AD上存在点P,使BP+ CP最小,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=16cm,DC=12cm,AD=21cm,点P以2cm/s的速度沿DA边由点D向点A运动,同时点Q以1cm/s的速度沿CB边由点C向点B运动,而且当其中一点停止运动时另一点也停止运动。设运功时间为t(s)
(1)用含t的代数式表示下面线段的长度:
①CQ=__________cm ; ②PD=__________cm
③BQ=__________cm ; ④AP=___________cm
(2)当t为_______s时,PQ∥AB
(3)是否存在某一时刻t,使得PQ⊥BD?若存在,求出t值;若不存在,请说明理由。

查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面方法,解答后面的问题:
(阅读理解)我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用。
例题:已知x可取任意实数,试求二次三项式![]() 的取值范围。
的取值范围。
解: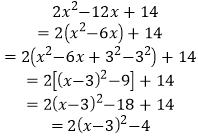
∵x取任何实数,总有![]() ,∴
,∴![]() 。
。
因此,无论x取任何实数,![]() 的值总是不小于-4的实数。
的值总是不小于-4的实数。
特别的,当x=3时,![]() 有最小值-4
有最小值-4
(应用1):已知x可取任何实数,则二次三项式![]() 的最值情况是( )
的最值情况是( )
A. 有最大值-10 B. 有最小值-10 C. 有最大值-7 D. 有最小值-7
(应用2):某品牌服装进货价为每件50元,商家在销售中发现:当以每件90元销售时,平均每天可售出20件,为了扩大销售量,增加盈利,商家决定采取适当的降价措施。
(1)将市场调查发现:如果每件服装降价1元,那么平均每天那就可多售出2件,要想平均每天销售这种服装盈利为1200元,我们设降价x元,根据题意列方程得( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
(2)请利用上面(阅读理解)提供的方法解决下面问题:
这家服装专柜为了获得每天的最大盈利,每件服装需要降价多少元?每天的最大盈利又是多少元?
查看答案和解析>>
科目: 来源: 题型:
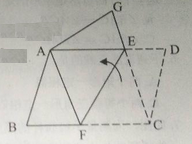
【题目】如图,将一张平行四边形纸片ABCD沿着线段EF折叠(点E、F分别在AB边和BC边上),使得点C落在点A处,点D落在点G出。
(1)如果连接EC,那么线段GE与EC在同一条直线上吗?为什么?
(2)试判断四边形AFCE的形状,并说明你是怎样判断的?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在一个不透明的口袋中装有3个红球和一个白球,它们除了颜色外其他都相同。
(1)若从这个口袋中随机地取出1个球,则“取出的球恰好是白球”的概率是_______;
(2)若从这个口袋中随机地一次性取出2个球,再问问先用树状图或者列表的方法得到所有的结果,然后再求“取出的2个球恰好都是红球”的概率是多少?
(3)若往这个口袋中又加入了与袋中红球一样的若干个红球,在搅匀袋子之后,进行下面随机试验:随机地抽取1个球,记录它的颜色后又放回口袋中,......,我们如此很多次重复做这个试验后发现,取出红球的频率一直稳定在95%附近,那么请你求一下大约又加入了多少个红球?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程![]()
(1)当m___________时,已知方程为一元一次方程;
(2)当m___________时,已知方程为一元二次方程;
(3)若已知方程有实数根,求m的取值范围。
查看答案和解析>>
科目: 来源: 题型:
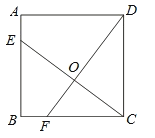
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,CE,DF交于点O,下面结论:(1)∠DOC=90°;(2)OC=OE ;(3)S△ODC=S四边形BEOF.
其中正确的有____________(只填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com