
科目: 来源: 题型:
【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:![]() >0.
>0.
解:设![]() =0,解得:
=0,解得:![]() =0,
=0,![]() =5,则抛物线y=
=5,则抛物线y=![]() 与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=
与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=![]() 的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即![]() >0,所以,一元二次不等式
>0,所以,一元二次不等式![]() >0的解集为:x<0或x>5.
>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式![]() <0的解集为 .
<0的解集为 .
(3)用类似的方法解一元二次不等式:![]() >0.
>0.
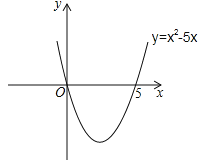
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将平行四边形ABCD绕点A逆时针旋转40°,得到平行四边形AB′C′D′,若点B′恰好落在BC边上,则∠DC′B′的度数为( )
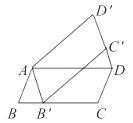
A. 60° B. 65° C. 70° D. 75°
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目: 来源: 题型:
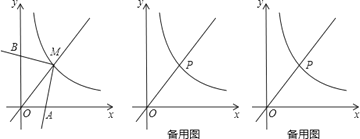
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(1)求k的值;
(2)点P在反比例函数y=![]() (x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
(x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数![]() 的图象经过点
的图象经过点![]() .
.
(1)若函数图象经过原点,求k,b的值
(2)若点![]() 是该函数图象上的点,当
是该函数图象上的点,当![]() 时,总有
时,总有![]() ,且图象不经过第三象限,求k的取值范围.
,且图象不经过第三象限,求k的取值范围.
(3)点![]() 在函数图象上,若
在函数图象上,若![]() ,求n的取值范围.
,求n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
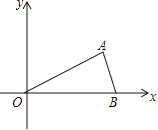
【题目】(9分)如图,在平面直角坐标系中,点A(![]() ,1)、B(2,0)、O(0,0),反比例函数y=
,1)、B(2,0)、O(0,0),反比例函数y=![]() 图象经过点A.
图象经过点A.
(1)求k的值;
(2)将△AOB绕点O逆时针旋转60°,得到△COD,其中点A与点C对应,试判断点D是否在该反比例函数的图象上?
查看答案和解析>>
科目: 来源: 题型:
【题目】杨梅是漳州的特色时令水果,杨梅一上市,某水果店的老板用1 200元购进一批杨梅,很快售完;该老板又用2 500元购进第二批杨梅,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批杨梅每件进价是多少元?
(2)老板以每件150元的价格销售第二批杨梅,售出80%后,为了尽快售完,决定打折促销,要使第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折?(利润=售价-进价)
查看答案和解析>>
科目: 来源: 题型:
【题目】某校要从新入学的两名体育特长生李勇、张浩中挑选一人参加校际跳远比赛,在跳远专项测试以及以后的![]() 次跳远选拔赛中,他们的成绩(单位:
次跳远选拔赛中,他们的成绩(单位:![]() )如下表所示:
)如下表所示:
专项测试和 | 平均数 | 方差 | |||||||
李勇 |
|
|
|
|
|
|
|
| |
张浩 |
|
|
|
|
|
|
|
| |
![]() 求张浩同学
求张浩同学![]() 次测试成绩的平均数,李勇同学
次测试成绩的平均数,李勇同学![]() 次测试成绩的方差;
次测试成绩的方差;
![]() 请你分别从平均数和方差的角度分析两人成绩的特点;
请你分别从平均数和方差的角度分析两人成绩的特点;
![]() 经查阅历届比赛的资料,成绩若达到
经查阅历届比赛的资料,成绩若达到![]() ,就很可能得到冠军,你认为应选谁去参赛夺冠军比较有把握?说明理由;
,就很可能得到冠军,你认为应选谁去参赛夺冠军比较有把握?说明理由;
![]() 以往的该项最好成绩的纪录是
以往的该项最好成绩的纪录是![]() ,若要想打破纪录,你认为应选谁去参赛?
,若要想打破纪录,你认为应选谁去参赛?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com