
科目: 来源: 题型:
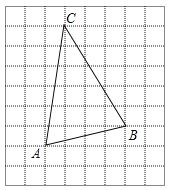
【题目】(2017天津)如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(1)AB的长等于____;
(2)在△ABC的内部有一点P,满足S△PS△PS△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)_______
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4 cm,面积为12 cm2,腰AB的垂直平分线EF交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM的周长最小值为( )
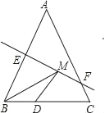
A. 5 cm B. 6 cm C. 8 cm D. 10 cm
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
问题情境
如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ;
;
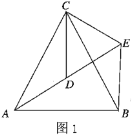
探究发现
(1)善思组发现:![]() ,请你帮他们写出推理过程;
,请你帮他们写出推理过程;
(2)钻研组受善思组的启发,求出了![]() 度数,请直接写出
度数,请直接写出![]() 等于______度;
等于______度;
(3)奋进组在前面两组的基础上又探索出了![]() 与
与![]() 的位置关系为______(请直接写出结果);
的位置关系为______(请直接写出结果);
拓展探究
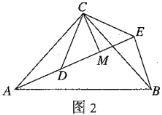
(4)如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,点
,点![]() ,
,![]() ,
,![]() 在同一条直线上,
在同一条直线上,![]() 为
为![]() 中
中![]() 边上的高,连接
边上的高,连接![]() ,试探究
,试探究![]() ,
,![]() ,
,![]() 之间有怎样的数量关系.
之间有怎样的数量关系.
创新组类比善思组的发现,很快证出![]() ,进而得出
,进而得出![]() .请你写出
.请你写出![]() ,
,![]() ,
,![]() 之间的数量关系并帮创新组完成后续的证明过程.
之间的数量关系并帮创新组完成后续的证明过程.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,并完成相应的任务:
杨辉三角
我国著名数学家华罗庚曾在给青少年撰写的“数学是我国人民所擅长的学科”一文中谈到,我国古代数学的许多创新与发展都曾居世界前列,他说:“实际上我们祖国伟大人民在人类史上,有过无比睿智的成就.”其中“杨辉三角”就是一例.
在我国南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,给出了二项式![]() 的展开式(按
的展开式(按![]() 的次数由大到小的顺序排列)及其系数规律.
的次数由大到小的顺序排列)及其系数规律.
如图所示
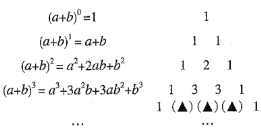
任务:(1)通过观察,图中的(▲)中可填入的数字依次为______、______、______;
(2)请直接写出![]() 的展开式:
的展开式:![]() ______;
______;
(3)根据(2)中的规律,求![]() 的值,写出计算过程.
的值,写出计算过程.
查看答案和解析>>
科目: 来源: 题型:
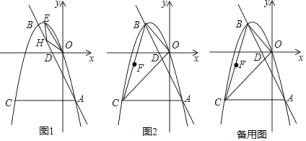
【题目】如图![]() ,抛物线
,抛物线![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,过
两点,过![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
![]() 求
求![]() 、
、![]() 、
、![]() 三点的坐标;
三点的坐标;
![]() 若点
若点![]() 是线段
是线段![]() 上的一个动点,过
上的一个动点,过![]() 作
作![]() 轴交抛物线于
轴交抛物线于![]() 点,连接
点,连接![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
![]() 如图
如图![]() ,连接
,连接![]() ,
,![]() 及
及![]() ,设点
,设点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上任意一点,将
上任意一点,将![]() 沿边
沿边![]() 翻折得到
翻折得到![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 与
与![]() 重叠部分的面积是
重叠部分的面积是![]() 面积的
面积的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com