
科目: 来源: 题型:
【题目】某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(1)直接写出y与x的函数关系式: .
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
查看答案和解析>>
科目: 来源: 题型:
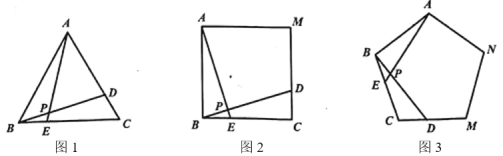
【题目】如图1、2、3中,点![]() 、
、![]() 分别是正
分别是正![]() 、正方形
、正方形![]() 、正五边形
、正五边形![]() 中以
中以![]() 点为顶点的相邻两边上的点,且
点为顶点的相邻两边上的点,且![]() ,
,![]() 交
交![]() 于
于![]() 点,
点,![]() 的度数分别为
的度数分别为![]() ,
,![]() ,
,![]() ,若其余条件不变,在正九边形
,若其余条件不变,在正九边形![]() 中,
中,![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方。即如果一个直角三角形的两条直角边长度分别是![]() 和
和![]() ,斜边长度是
,斜边长度是![]() ,那么
,那么![]() 。
。

(1)直接填空:如图①,若a=3,b=4,则c= ;若![]() ,
,![]() ,则直角三角形的面积是 ______ 。
,则直角三角形的面积是 ______ 。
(2)观察图②,其中两个相同的直角三角形边AE、EB在一条直线上,请利用几何图形的之间的面积关系,试说明![]() 。
。
(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长?
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题发现:如图1,![]() 和
和![]() 均为等边三角形,点
均为等边三角形,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,求证:
,求证:![]() .
.

(2)类比探究:如图2,![]() 和
和![]() 均为等腰直角三角形,
均为等腰直角三角形,![]() ,
,![]() 点在边
点在边![]() 的延长线上,连接
的延长线上,连接![]() .请判断:①
.请判断:①![]() 的度数为_________.②线段
的度数为_________.②线段![]() 之间的数量关系是_________.
之间的数量关系是_________.
(3)问题解决:在(2)中,如果![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
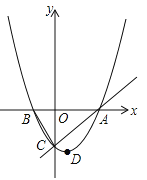
【题目】【本小题满分11分】如图,已知抛物线![]() 的顶点D的坐标为(1,
的顶点D的坐标为(1,![]() ),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
),且与x轴交于A、B两点,与y轴交于C点,A点的坐标为(4,0).P点是抛物线上的一个动点,且横坐标为m.
(l)求抛物线所对应的二次函数的表达式;
(2)若动点P满足∠PAO不大于45°,求P点的横坐标m的取值范围;
(3)当P点的横坐标![]() 时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
时,过p点作y轴的垂线PQ,垂足为Q.问:是否存在P点,使∠QPO=∠BCO?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
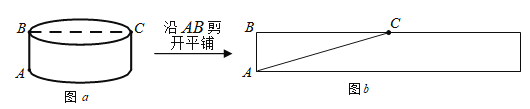
【题目】如图![]() ,圆柱的底面半径为
,圆柱的底面半径为![]() ,圆柱高
,圆柱高![]() 为
为![]() ,
,![]() 是底面直径,求一只蚂蚁从点
是底面直径,求一只蚂蚁从点![]() 出发沿圆柱表面爬行到点
出发沿圆柱表面爬行到点![]() 的最短路线,小明设计了两条路线:
的最短路线,小明设计了两条路线:
路线1:高线![]() 底面直径
底面直径![]() ,如图
,如图![]() 所示,设长度为
所示,设长度为![]() .
.
路线2:侧面展开图中的线段![]() ,如图
,如图![]() 所示,设长度为
所示,设长度为![]() .
.
请按照小明的思路补充下面解题过程:
(1)解:![]()
![]() ;
;
![]()
(2)小明对上述结论有些疑惑,于是他把条件改成:“圆柱底面半径为![]() ,高
,高![]() 为
为![]() ”继续按前面的路线进行计算.(结果保留
”继续按前面的路线进行计算.(结果保留![]() )
)
①此时,路线1:__________.路线2:_____________.
②所以选择哪条路线较短?试说明理由.
查看答案和解析>>
科目: 来源: 题型:
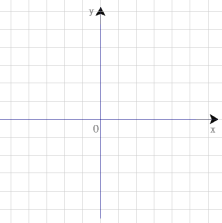
【题目】抛物线y=![]() 与y轴交于(0,3)点.
与y轴交于(0,3)点.
(1)求出m的值并在给出的直角坐标系中画出这条抛物线;
(2)根据图像回答下列问题:
①方程![]() 的根是多少?
的根是多少?
②x取什么值时,![]() ?
?
查看答案和解析>>
科目: 来源: 题型:
【题目】探究应用:
(1)计算:![]() ___________;
___________;![]() ______________.
______________.
(2)上面的乘法计算结果很简洁,你发现了什么规律(公式)?用含字母![]() 的等式表示该公式为:_______________.
的等式表示该公式为:_______________.
(3)下列各式能用第(2)题的公式计算的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com