
科目: 来源: 题型:
【题目】已知如图![]() ,在以
,在以![]() 为原点的平面直角坐标系中,抛物线
为原点的平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,直线
,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴,
轴,![]() ,
,
![]() 求抛物线对应的二次函数的解析式;
求抛物线对应的二次函数的解析式;
![]() 若
若![]() 为抛物线
为抛物线![]() 上一动点,是否存在直线
上一动点,是否存在直线![]() 使得点
使得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长恒相等?若存在,求出此时
的长恒相等?若存在,求出此时![]() 的值;
的值;
![]() 如图
如图![]() ,若
,若![]() 、
、![]() 为上述抛物线上的两个动点,且
为上述抛物线上的两个动点,且![]() ,线段
,线段![]() 的中点为
的中点为![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】小红爸爸从家骑电瓶车出发,沿一条直路到相距2400m的学校接小红回家,小红爸爸出发的同时,小红以96m/min的速度从学校沿同一条道路步行回家,小红爸爸赶到学校校门口等候2min后知道小红已离校,立即沿原路以原速返回,设他们出发的时间为t min,图示中的折线OABD表示小红爸爸与家之间的距离S1与t之间的函数关系,线段EF表示小红与家之间的距离S2与t之间的函数关系,则小红爸爸从家出发在返回途中追上小红的时间是( )
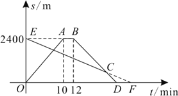
A.12minB.16minC.18minD.20min
查看答案和解析>>
科目: 来源: 题型:
【题目】某水果店销售一种水果的成本价是![]() 元/千克.在销售过程中发现,当这种水果的价格定在
元/千克.在销售过程中发现,当这种水果的价格定在![]() 元/千克时,每天可以卖出
元/千克时,每天可以卖出![]() 千克.在此基础上,这种水果的单价每提高
千克.在此基础上,这种水果的单价每提高![]() 元/千克,该水果店每天就会少卖出
元/千克,该水果店每天就会少卖出![]() 千克.
千克.
![]() 若该水果店每天销售这种水果所获得的利润是
若该水果店每天销售这种水果所获得的利润是![]() 元,则单价应定为多少?
元,则单价应定为多少?
![]() 在利润不变的情况下,为了让利于顾客,单价应定为多少?
在利润不变的情况下,为了让利于顾客,单价应定为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 、
、![]() 、
、![]() 、
、![]() 为矩形的四个顶点,
为矩形的四个顶点,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以
以![]() 的速度向点
的速度向点![]() 移动,一直到达
移动,一直到达![]() 为止,点
为止,点![]() 以
以![]() 的速度向
的速度向![]() 移动.
移动.
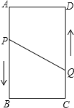
![]() 、
、![]() 两点从出发开始到几秒?四边形
两点从出发开始到几秒?四边形![]() 的面积为
的面积为![]() ;
;
![]() 、
、![]() 两点从出发开始到几秒时?点
两点从出发开始到几秒时?点![]() 和点
和点![]() 的距离是
的距离是![]() .
.
查看答案和解析>>
科目: 来源: 题型:
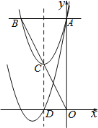
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与过点
,与过点![]() 平行于
平行于![]() 轴的直线相交于点
轴的直线相交于点![]() (点
(点![]() 在第二象限),抛物线的顶点
在第二象限),抛物线的顶点![]() 在直线
在直线![]() 上,且点
上,且点![]() 为
为![]() 的中点,对称轴与
的中点,对称轴与![]() 轴相交于点
轴相交于点![]() ,平移抛物线,使其经过点
,平移抛物线,使其经过点![]() 、
、![]() ,则平移后的抛物线的解析式为________.
,则平移后的抛物线的解析式为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了防止水土流失,某村开展绿化荒山活动,计划经过若干年使本村绿化总面积新增360万平方米.自2014年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.问实际每年绿化面积多少万平方米?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知顶点为(-3,-6)的抛物线![]() 经过点(-1,-4),下列结论中错误的是( )
经过点(-1,-4),下列结论中错误的是( )

A. ![]()
B. 若点(-2, ![]() ),(-5,
),(-5, ![]() ) 在抛物线上,则
) 在抛物线上,则![]()
C. ![]()
D. 关于![]() 的一元二次方程
的一元二次方程![]() 的两根为-5和-1
的两根为-5和-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com