
科目: 来源: 题型:
【题目】勾股定理是数学中最常见的定理之一,熟练的掌握勾股数,对迅速判断、解答题目有很大帮助,观察下列几组勾股数:
|
|
| |
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
| |
… | … | … | … |
|
|
|
|
(1)你能找出它们的规律吗?(填在上面的横线上)
(2)你能发现![]() ,
,![]() ,
,![]() 之间的关系吗?
之间的关系吗?
(3)对于偶数,这个关系 (填“成立”或“不成立”)吗?
(4)你能用以上结论解决下题吗?
![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校初二年级在元旦汇演中需要外出租用同一种服装若干件,已知在没有任何优惠的情况下,同时在甲服装店租用2件和乙服装店租用3件共需280元,在甲服装店租用4件和乙服装店租用一件共需260元.
(1)求两个服装店提供的单价分别是多少?
(2)若该种服装提前一周订货则甲乙两个租售店都可以给予优惠,具体办法如下:甲服装店按原价的八折进行优惠;在乙服装店如果租用5件以上,则超出5件的部分可按原价的六折进行优惠;设需要租用![]() (
(![]() )件服装,选择甲店则需要
)件服装,选择甲店则需要![]() 元,选择乙店则需要
元,选择乙店则需要![]() 元,请分别求出
元,请分别求出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)若租用的服装在5件以上,请问租用多少件时甲乙两店的租金相同?
查看答案和解析>>
科目: 来源: 题型:
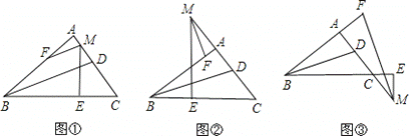
【题目】小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就图①、图②、或图③中的一种情况,给出证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=ax2+bx+![]() (a>0,b<0)的图象与x轴只有一个公共点A
(a>0,b<0)的图象与x轴只有一个公共点A
(1)当a=![]() 时,求点A的坐标;
时,求点A的坐标;
(2)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥﹣1时,求点B的横坐标m的取值范围
查看答案和解析>>
科目: 来源: 题型:
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员举行了一次选拔赛,要求这两名队员各射击10次.比赛结束后,根据比赛成绩情况,将甲、乙两名队员的比赛成绩制成了如下的统计表:
甲队员成绩统计表
成绩(环) | 7 | 8 | 9 | 10 |
次数(次) | 5 | 1 | 2 | 2 |
乙队员成绩统计表
成绩(环) | 7 | 8 | 9 | 10 |
次数(次) | 4 | 3 | 2 | 1 |
(1)经过整理,得到的分析数据如表,求表中的![]() ,
,![]() ,
,![]() 的值.
的值.
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 |
|
乙 |
|
| 7 | 1 |
(2)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一条笔直的公路上有![]() 两地,甲,乙两辆货车都要从
两地,甲,乙两辆货车都要从![]() 地送货到
地送货到![]() 地,甲车先从
地,甲车先从![]() 地出发匀速行驶,3小时后乙车从
地出发匀速行驶,3小时后乙车从![]() 地出发,并沿同一路线匀速行驶,当乙车到达
地出发,并沿同一路线匀速行驶,当乙车到达![]() 地后立刻按原速返回,在返回途中第二次与甲车相遇,甲车出发的时间记为
地后立刻按原速返回,在返回途中第二次与甲车相遇,甲车出发的时间记为![]() (小时),两车之间的距离记为
(小时),两车之间的距离记为![]() (千米),
(千米),![]() 与
与![]() 的函数关系如图所示,则乙车第二次与甲车相遇是甲车距离
的函数关系如图所示,则乙车第二次与甲车相遇是甲车距离![]() 地( )千米.
地( )千米.
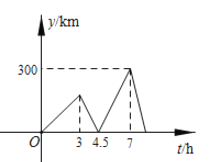
A.495B.505C.515D.525
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC,∠ACB=90°,AC=BC=4,D是AB的中点,P是平面上的一点,且DP=1,连接BP,CP
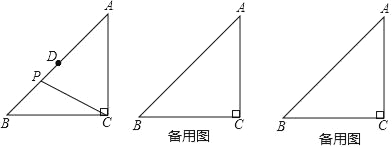
(1)如图,当点P在线段BD上时,求CP的长;
(2)当△BPC是等腰三角形时,求CP的长;
(3)将点B绕点P顺时针旋转90°得到点B′,连接AB′,求AB′的最大值.
查看答案和解析>>
科目: 来源: 题型:
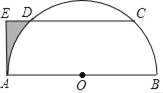
【题目】如图,AB是半圆O的直径,C,D是半圆O上的两点,弧AC=弧BD,AE与弦CD的延长线垂直,垂足为E.
(1)求证:AE与半圆O相切;
(2)若DE=2,AE=![]() ,求图中阴影部分的面积
,求图中阴影部分的面积
查看答案和解析>>
科目: 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com