
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,点C关于抛物线对称轴的对称点为点D,抛物线顶点为H(1,2).
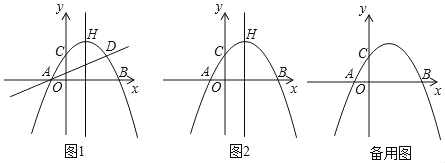
(1)求抛物线的解析式;
(2)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在一动点Q,使PQ+![]() QB最小,求此时点Q的坐标及PQ+
QB最小,求此时点Q的坐标及PQ+![]() QB的最小值;
QB的最小值;
(3)若点E为抛物线上的动点,点G,F为平面内的点,以BE为边构造以B,E,F,G为顶点的正方形,当顶点F或者G恰好落在y轴上时,求点E的横坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,任意画一个∠BAC=60°的△ABC,再分别作△ABC的两条角平分线BE和CD,BE和CD相交于点P,连接AP,有以下结论:①∠BPC=120°;②AP平分∠BAC;③AD=AE;④PD=PE;⑤BD+CE=BC;其中正确的结论为_____.(填写序号)
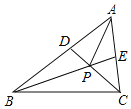
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE﹣ED﹣DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒,设P、Q同时出发t秒时,△BPQ的面积为ycm2,已知y与t的函数关系图象如图2所示,请回答:
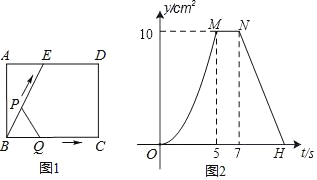
(1)线段BC的长为 cm.
(2)当运动时间t=2.5秒时,P、Q之间的距离是 cm.
查看答案和解析>>
科目: 来源: 题型:
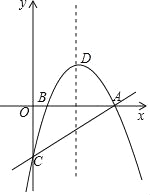
【题目】如图,抛物线y=ax2+bx+c与x轴交于A,B(1,0)两点,与y轴交于点C,直线y=![]() x﹣2经过A,C两点,抛物线的顶点为D.
x﹣2经过A,C两点,抛物线的顶点为D.
(1)求抛物线的解析式及顶点D的坐标;
(2)在直线AC上方的抛物线上存在一点P,使△PAC的面积最大,请直接写出P点坐标及△PAC面积的最大值;
(3)在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若![]() ,则△A6B6A7的边长为( )
,则△A6B6A7的边长为( )
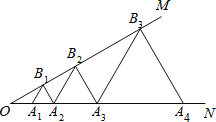
A.6B.12C.16D.32
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
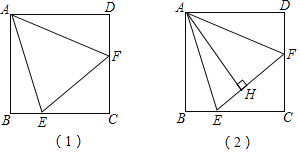
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
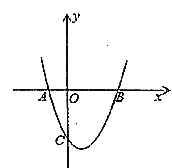
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】点D是△ABC中∠BAC的平分线和BC的垂直平分线的交点,DG⊥AB于点G,DH⊥AC交AC的延长线于点H.
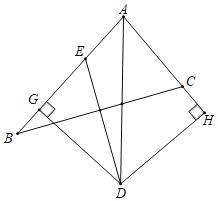
(1)求证:BG=CH;
(2)若AB=12,AC=6,则BG= .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中AB=AC,△AED中AE=AD,∠EAD=∠BAC,AC与BD交于点O.
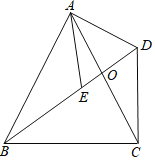
(1)试确定∠ADC与∠AEB间的数量关系,并说明理由;
(2)若∠ACB=65°,求∠BDC的度数.
查看答案和解析>>
科目: 来源: 题型:
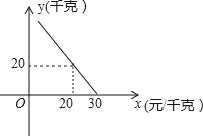
【题目】五家尧草莓是我旗的特色农产品,深受人们的喜欢.某超市对进货价为10元/千克的某种草莓的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)为了让顾客得到实惠,商场将销售价定为多少时,该品种草莓每天销售利润为150元?
(3)应怎样确定销售价,使该品种草莓的每天销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com