
科目: 来源: 题型:
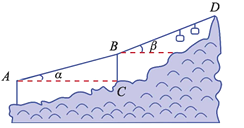
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,斜边
中,斜边![]() 的中垂线
的中垂线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,
,![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 的延长线与点
的延长线与点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,现有不列结论:①
,现有不列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中正确的个数是( )
,其中正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
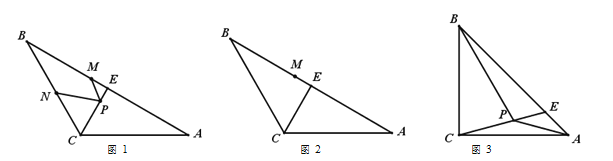
【题目】在△ABC 中,AC=BC,点 E 在是 AB 边上一动点(不与 A、B 重合),连接 CE,点 P 是直线 CE 上一个动点.
(1)如图 1,∠ACB=120°,AB=16,E 是 AB 中点,EM=2,N 是射线 CB 上一个动点, 若使得 NP+MP 的值最小,应如何确定 M 点和点 N 的位置?请你在图 2 中画出点 M 和点 N 的位置,并简述画法: 直接写出 NP+MP 的最小值
(2)如图 3,∠ACB=90°,连接 BP, BPC=75°且 BC=BP.求证:PC=PA.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,CN是等边△![]() 的外角
的外角![]() 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(3)用等式表示线段![]() ,
, ![]() 与
与![]() 之间的数量关系,并证明.
之间的数量关系,并证明.

查看答案和解析>>
科目: 来源: 题型:
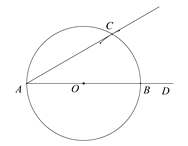
【题目】下面是“作一个角等于30°”的尺规作图过程.
作法:如图,(1)作射线AD;
(2)在射线AD上任意取一点O(点O不与点A重合);
(3)以点O为圆心,OA为半径作⊙O,交射线AD于点B;
(4)以点B为圆心,OB为半径作弧,交⊙O于点C;
(5)作射线AC.
∠DAC即为所求作的30°角.
请回答:该尺规作图的依据是_________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践
问题情境:正方形折叠中的数学
已知正方形纸片ABCD中,AB=4,点E是AB边上的一点,点G是CE的中点,将正方形纸片沿CE所在直线折叠,点B的对应点为点B′.
(1)如图1,当∠BCE=30°时,连接BG,B′G,求证:四边形BEB′G是菱形;
深入探究:
(2)在CD边上取点F,使DF=BE,点H是AF的中点,再将正方形纸片ABCD沿AF所在直线折叠,点D的对应点为D′,顺次连接B′,G,D′,H,B',得到四边形B′GD′H.
请你从A,B两题中任选一题作答,我选择 题.
A题:如图2,当点B',D′均落在对角线AC上时,
①判断B′G与D′H的数量关系与位置关系,并说明理由;
②直写出此时点H,G之间的距离.
B题:如图3,点M是AB的中点,MN∥BC交CD于点N,当点B',D′均落在MN上时,
①判断B′G与D′H的数量关系与位置关系,并说明理由;
②直接写出此时点H,G之间的距离.

查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,A(m,0)为 x 轴负半轴上的点,B(0,n)为 y 轴负半轴上的点.
(1)如图,以 A 点为顶点,AB 为腰在第三象限作等腰 Rt△ABC.若已知 m= 2,n= 4,试求 C 点的坐标;
(2)若∠ACB=90°,点 C 的坐标为(4, 4),请在坐标系中画出图形并求 n﹣m 的值.

查看答案和解析>>
科目: 来源: 题型:
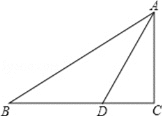
【题目】已知:如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AD 平分∠BAC.
(1)求证:点 D 在 AB 的垂直平分线上;
(2)若 CD=2,求 BC 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,点 A(0,8),点 B(6,8).
(1)尺规作图:求作一个点 P,使点 P 同时满足下列两个条件(要求保留作图痕迹,不必写出作法)
①点 P 到 A,B 两点的距离相等;
②点 P 到∠xOy 的两边的距离相等;
(2)在(1)作出点 P 后,直接写出点 P 的坐标 .

查看答案和解析>>
科目: 来源: 题型:
【题目】当题目条件出现角平分线时,我们往往可以构造等腰三角形解决问题.如图1,在△ABC中,∠A=2∠B,CD 平分∠ACB,AD=2,AC=3,求 BC 的长.解决方法:如图 2,在BC 边上取点 E,使 EC=AC,连接 DE.可得△DEC≌△DAC 且△BDE 是等腰三角形,所以 BC 的长为 5.试通过构造等腰三角形解决问题:如图 3,△ABC 中,AB=AC,∠A=20°,BD 平分∠ABC,要想求 AD 的长,仅需知道下列哪些线段的长(BC=a, BD=b, DC=c)

A.a 和 bB.a 和 cC.b 和 cD.a、b 和 c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com