
科目: 来源: 题型:
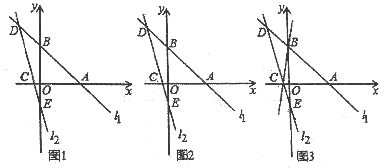
【题目】如图 1,在平面直角坐标系中,直线l1:yx5与x轴,y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(-3,8)且与x轴,y轴分别交于C、E.
(1)求出点A坐标,直线l2的解析式;
(2)如图2,点P为线段AD上一点(不含端点),连接CP,一动点Q从C出发,沿线段CP 以每秒1个单位的速度运动到点P,再沿着线段PD以每秒![]() 个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
个单位的速度运动到点D停止,求点Q在整个运动过程中所用最少时间与点P的坐标;
(3)如图3,平面直角坐标系中有一点G(m,2),使得SCEGSCEB,求点G的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D在边AB上,点E在边AC的左侧,连接AE.
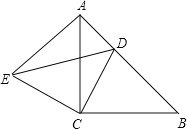
(1)求证:AE=BD;
(2)试探究线段AD、BD与CD之间的数量关系;
(3)过点C作CF⊥DE交AB于点F,若BD:AF=1:2![]() ,CD=
,CD=![]() ,求线段AB的长.
,求线段AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过A(0,2),B(2,﹣2)两点.
⑴用含a的式子表示b.
⑵当a=﹣![]() 时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
时,y=ax2+bx+c的函数值为正整数,求满足条件的x值.
⑶若a>0,线段AB下方的抛物线上有一点E,求证:不管a取何值,当△EAB的面积最大时,E点的横坐标为定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知AB⊥BC,CD⊥BC,AB=4,CD=2.P为线段BC上的点,设BC=m.
⑴若m=9,
①若△BAP∽△CDP,求线段BP的长;
②若△BAP∽△CPD,求线段BP的长;
⑵试求m为何值时,使得△BAP与△CDP相似的点P有且只有2个.

查看答案和解析>>
科目: 来源: 题型:
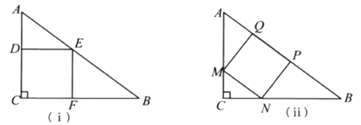
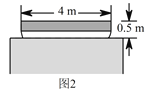
【题目】一块直角三角形的木板,它的一条直角边AC长为1.5米,面积为1.5平方米.现在要把它加工成一个正方形桌面,甲、乙两人的加工方法分别如图(ⅰ)、(ⅱ)所示,记两个正方形面积分别为S1、S2,请通过计算比较S1与S2的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.
⑴用含t的代数式表示:AP= ,AQ= .
⑵当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?

查看答案和解析>>
科目: 来源: 题型:
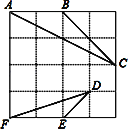
【题目】如图,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
⑴填空:∠ABC= °,AC= ;
⑵判断:△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
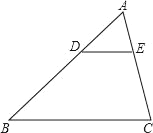
【题目】如图,已知△ABC∽△ADE,AB=30cm,BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°.
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某服务厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:(I)买一套西装送一条领带;(II)西装和领带均按定价的90%付款.某超市经理现要到该服务厂购买西装20套,领带若干条(不少于20条).
(1)设购买领带为x(条),采用方案I购买时付款数为y1(元),采用方案II购买时付款数为![]() (元).分别写出采用两种方案购买时付款数与领带条数x之间的函数关系式;
(元).分别写出采用两种方案购买时付款数与领带条数x之间的函数关系式;
(2)就领带条数x讨论在上述方案中采用哪种方案购买合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com