
科目: 来源: 题型:
【题目】黄岩某校搬迁后,需要增加教师和学生的寝室数量,寝室有三类,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2018年学校寝室数为64个,以后逐年增加,预计2020年寝室数达到121个,求2018至2020年寝室数量的年平均增长率;
(2)若三类不同的寝室的总数为121个,则最多可供多少师生住宿?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在等边△ABC中,点D,E分別在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
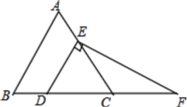
(1)求∠F的度数;
(2)若CD=2,求DF、EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目: 来源: 题型:
【题目】点P(a,b)是直线y=-x-5与双曲线![]() 的一个交点,则以a、b两数为根的一元二次方程是( ).
的一个交点,则以a、b两数为根的一元二次方程是( ).
A. x2-5x+6=0 B. x2+5x+6=0 C. x2-5x-6="0" D. x2+5x-6=0
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,![]() 是以
是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为
为![]() 的中点,点
的中点,点![]() 、
、![]() 、
、![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 上的一点,
上的一点,![]() 以
以![]() 为直角顶点的等腰直角三角形,
为直角顶点的等腰直角三角形,![]() ,连结
,连结![]() .
.
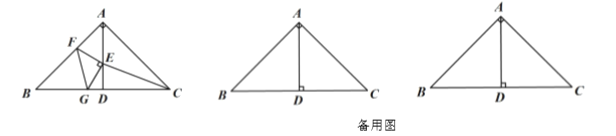
(1)当![]() 与点
与点![]() 重合时,求
重合时,求![]() 的长.
的长.
(2)当![]() 时,求
时,求![]() 的面积.
的面积.
(3)①比较![]() 与
与![]() 的面积大小关系,并说明理由.
的面积大小关系,并说明理由.
②当![]() 的面积为6时,求
的面积为6时,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知![]() 为正方形
为正方形![]() 的中心,分别延长
的中心,分别延长![]() 到点
到点![]() ,
, ![]() 到点
到点![]() ,使
,使![]() ,
, ![]() ,连结
,连结![]() ,将△
,将△![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角得到△
角得到△![]() (如图2).连结
(如图2).连结![]() 、
、![]() .
.
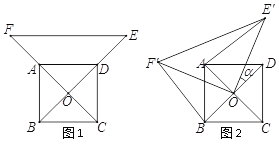
(Ⅰ)探究![]() 与
与![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(Ⅱ)当![]() ,
, ![]() 时,求:
时,求:
①![]() 的度数;
的度数;
②![]() 的长度.
的长度.
查看答案和解析>>
科目: 来源: 题型:
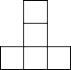
【题目】用若干个小立方块搭成一个几何体,使它从正面看与从左面看都是如图的同一个图.通过实际操作,并与同学们讨论,解决下列问题:
(1)所需要的小立方块的个数是多少?你能找出几种?
(2)画出所需个数最少和所需个数最多的几何体从上面看到的图,并在小正方形里注明在该位置上小立方块的个数.
查看答案和解析>>
科目: 来源: 题型:
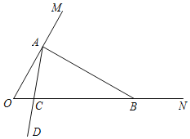
【题目】在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.
如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°< ∠OAC < 90°).
(1)∠ABO的度数为 °,△AOB (填“是”或“不是”灵动三角形);
(2)若∠BAC=60°,求证:△AOC为“灵动三角形”;
(3)当△ABC为“灵动三角形”时,求∠OAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com