
科目: 来源: 题型:
【题目】A、B两地相距20千米,甲、乙两人都从A地去B地,图中射线l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系.
下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时,乙的速度是6千米/小时;
④乙先到达B地.其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】某家电商场计划用9万元从生产厂家购进50台电视机,已知该厂家生产3种不同型号的电视机,出厂价分别为A种每台1500元,B种每台2100元,C种每台2500元.
(1)若家电商场同时购进两种不同型号的电视机共50台,用去9万元,请你计算一下商场有哪几种进货方案?
(2)若商场销售一台A种电视机可获利150元,销售一台B种电视机可获利200元,销售一台C种电视机可获利250元,在同时购进两种不同型号的电视机方案中,为了使销售时获利最多,应选择哪种方案?
查看答案和解析>>
科目: 来源: 题型:
【题目】)图①中是一座钢管混凝土系杆拱桥,桥的拱肋ACB可视为抛物线的一部分(如图②),桥面(视为水平的)与拱肋用垂直于桥面的系杆连接,测得拱肋
的跨度AB为200米,与AB中点O相距20米处有一高度为48米的系杆.
【1】求正中间系杆OC的长度;
【2】若相邻系杆之间的间距均为5米(不考虑系杆的粗细),则是否存在一根系杆的长度恰好是OC长度的一半?请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两人在一环形场地上锻炼,甲骑自行车,乙跑步,甲比乙每分钟快200m,两人同时从起点同向出发,经过3min两人首次相遇,此时乙还需跑150m才能跑完第一圈.
![]() 求甲、乙两人的速度分别是每分钟多少米?
求甲、乙两人的速度分别是每分钟多少米?![]() 列方程或者方程组解答
列方程或者方程组解答![]()
![]() 若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过
若两人相遇后,甲立即以每分钟300m的速度掉头向反方向骑车,乙仍按原方向继续跑,要想不超过![]() 两人再次相遇,则乙的速度至少要提高每分钟多少米?
两人再次相遇,则乙的速度至少要提高每分钟多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】先阅读下列的解题过程,然后回答下列问题.
例:解绝对值方程:![]() .
.
解:讨论:①当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() ;
;
②当![]() 时,原方程可化为
时,原方程可化为![]() ,它的解是
,它的解是![]() .
.
原方程的解为![]() 或
或![]() .
.
(1)依例题的解法,方程算![]() 的解是_______;
的解是_______;
(2)尝试解绝对值方程:![]() ;
;
(3)在理解绝对值方程解法的基础上,解方程:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,把![]() 放置在量角器上,
放置在量角器上,![]() 与量角器的中心重合,读得射线
与量角器的中心重合,读得射线![]() 、
、![]() 分别经过刻度
分别经过刻度![]() 和
和![]() ,把
,把![]() 绕点
绕点![]() 逆时针方向旋转到
逆时针方向旋转到![]() ,下列结论:
,下列结论:
①![]() ;
;
②若射线![]() 经过刻度
经过刻度![]() ,则
,则![]() 与
与![]() 互补;
互补;
③若![]() ,则射线
,则射线![]() 经过刻度45.
经过刻度45.
其中正确的是( )
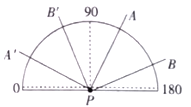
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目: 来源: 题型:
【题目】在阳光体育活动时间,小亮、小莹、小芳和大刚到学校乒乓球室打乒乓球,当时只有一副空球桌,他们只能选两人打第一场.
(1)如果确定小亮打第一场,再从其余三人中随机选取一人打第一场,求恰好选中大刚的概率;
(2)如果确定小亮做裁判,用“手心、手背”的方法决定其余三人哪两人打第一场.游戏规则是:三人同时伸“手心、手背”中的一种手势,如果恰好有两人伸出的手势相同,那么这两人上场,否则重新开始,这三人伸出“手心”或“手背”都是随机的,请用画树状图的方法求小莹和小芳打第一场的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在坐标平面内,点O是坐标原点,A(0,6),B(2![]() ,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
,0),且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
(1)求点C的坐标:
(2)动点P从点O出发,以2个单位长度/秒的速度沿线段OA向终点A运动,设△POB的面积为S(S≠0),点P的运动时间为t秒,求S与t的关系式,并直接写出t的取值范围.
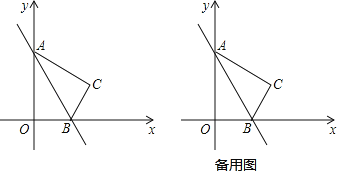
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在等边△ABC中,E、D两点分别在边AB、BC上,BE=CD,AD、CE相交于点F.
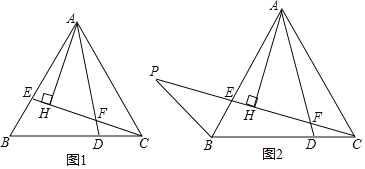
(1)求∠AFE的度数;
(2)过点A作AH⊥CE于H,求证:2FH+FD=CE;
(3)如图2,延长CE至点P,连接BP,∠BPC=30°,且CF=![]() CP,求
CP,求![]() 的值.
的值.
(提示:可以过点A作∠KAF=60°,AK交PC于点K,连接KB)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com