
科目: 来源: 题型:
【题目】综合探究:观察发现:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
…
建立模型:形如![]() 的化简(其中
的化简(其中![]() ,
,![]() 为正整数),只要我们找到两个正整数
为正整数),只要我们找到两个正整数![]() ,
,![]() (
(![]() ),使
),使![]() ,
,![]() ,那么
,那么![]() .问题解决:
.问题解决:
(1)根据观察证明“建立模型”的结论是正确的;
(2)化简:①![]() ;
;
②![]() ;
;
(3)已知一个长方形的长为![]() ,宽为
,宽为![]() ,若某正方形的面积与该长方形的面积相等,设正方形边长为
,若某正方形的面积与该长方形的面积相等,设正方形边长为![]() ,求正方形的边长.
,求正方形的边长.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料并回答问题.我们知道,![]() ,
,![]() ,…,如果两个含有二次根式的非零代数式相乘,它们的积不含二次根式,就说这两个非零代数式互为有理化因式.如
,…,如果两个含有二次根式的非零代数式相乘,它们的积不含二次根式,就说这两个非零代数式互为有理化因式.如![]() 与
与![]() 互为有理化因式,
互为有理化因式,![]() 和
和![]() 互为有理化因式.根据互为有理化因式的积是有理数,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化.例如:
互为有理化因式.根据互为有理化因式的积是有理数,可以将分母中含有二次根式的代数式化为分母是有理数的代数式,这个过程称为分母有理化.例如:![]() .请解答下列问题:
.请解答下列问题:
(1)![]() 分母有理化的结果是 ;
分母有理化的结果是 ;![]() 分母有理化的结果是 ;
分母有理化的结果是 ;
(2)计算:![]() ;
;
(3)若实数![]() ,
,![]() ,判断
,判断![]() 和
和![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
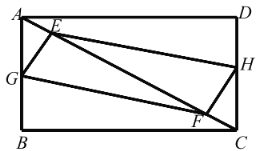
【题目】在矩形 ABCD 中,AB=3,BC=4,E、F 是对角线 AC 上的两个动点,分 别从 A、C 同时出发相向而行,速度均为每秒 1 个单位长度,运动时间为 t 秒,其中 0 t 5 .
(1)若 G,H 分别是 AB,DC 中点,求证:四边形 EGFH 是平行四边形(E、F 相遇时除外);
(2)在(1)条件下,若四边形 EGFH 为矩形,求 t 的值;
(3)若 G,H 分别是折线 A-B-C,C-D-A 上的动点,与 E,F 相同的速度同时出发,若 四边形 EGFH 为菱形,求 t 的值.
查看答案和解析>>
科目: 来源: 题型:
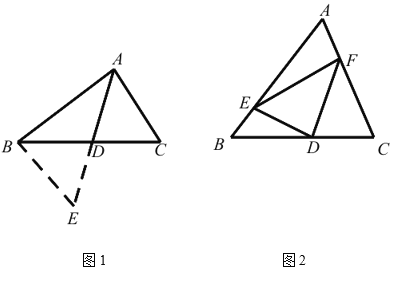
【题目】课外兴趣小组活动时,老师提出了如下问题:如图 1,在△ABC 中,若 AB=5,AC=3,求 BC 边上的中线 AD 的取值范围. 小明在组内经过合作交流,得到了如下的解决方法:延长 AD 到 E,使得 DE=AD,再连接 BE(或将△ACD 绕点 D 逆时针旋转 180°得到△EBD),把 AB、AC、2AD 集中在△ABE 中, 利用三角形的三边关系可得 2<AE<8,则 1<AD<4.
(感悟)解题时,条件中若出现中点、中线字样,可以考虑构造以中点为对称中心的中 心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(解决问题)受到(1)的启发,请你证明下列命题:如图 2,在△ABC 中,D 是 BC 边上的中点, DE⊥DF,DE 交 AB 于点 E,DF 交 AC 于点 F,连接 EF.
(1)求证:BE+CF>EF,
(2)若∠A=90°,探索线段 BE、CF、EF 之间的等量关系,并加以证明.、
查看答案和解析>>
科目: 来源: 题型:
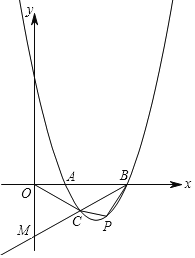
【题目】如图,抛物线y=a(x﹣1)(x﹣3)(a>0)与x轴交于A、B两点,抛物线上另有一点C在x轴下方,且使△OCA∽△OBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点M,点C是BM的中点时,求直线BM和抛物线的解析式;
(3)在(2)的条件下,直线BC下方抛物线上是否存在一点P,使得四边形ABPC面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
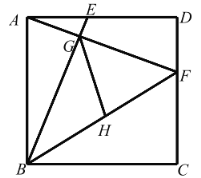
【题目】如图,已知正方形 ABCD 的边长为 5,点 E、F 分别在 AD、DC 上,AE=DF=2,BE 与 AF 相交于点 G,点 H 为 BF 的中点,连接 GH,求 GH 的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在□ABCD 中,以点 A 为圆心,AB 长为半径画弧交 AD 于点 F,再分别以点 B、F 为圆心,大于![]() BF 的相同长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点 E,连接 EF.
BF 的相同长为半径画弧,两弧交于点 P,连接 AP 并延长交 BC 于点 E,连接 EF.
(1)根据以上尺规作图的过程,证明四边形 ABEF 是菱形;
(2)若菱形 ABEF 的边长为 2,AE= 2 ![]() ,求菱形 ABEF 的面积.
,求菱形 ABEF 的面积.

查看答案和解析>>
科目: 来源: 题型:
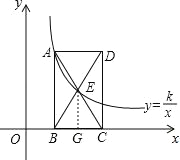
【题目】已知如图:点(1,3)在函数y=![]() (x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
(x>0)的图象上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点A的坐标;(用含m代数式表示)
(3)当∠ABD=45°时,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC绕点O逆时针旋转90°后的△A1B1C1.
(2)将△ABC向右平移3个单位,作出平移后的△A2B2C2.
(3)若点M是平面直角坐标系中直线AB上的一个动点,点N是x轴上的一个动点,且以O、A2、M、N为顶点的四边形是平行四边形,请直接写出点N的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com