
科目: 来源: 题型:
【题目】第二十四届冬季奥林匹克运动会将于2022年在北京市和张家口市举行.为了调查学生对冬奥知识的了解情况,从甲、乙两校各随机抽取20名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲校20名学生成绩的频数分布表和频数分布直方图如下:
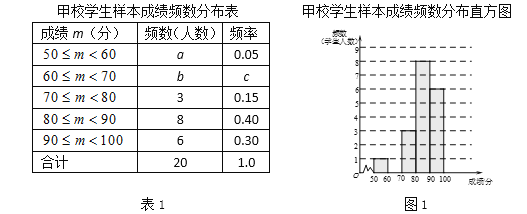
b.甲校成绩在![]() 的这一组的具体成绩是:
的这一组的具体成绩是:
87 88 88 88 89 89 89 89
c.甲、乙两校成绩的平均分、中位数、众数、方差如下:
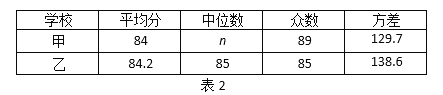
根据以上图表提供的信息,解答下列问题:
(1)表1中a = ;表2中的中位数n = ;
(2)补全图1甲校学生样本成绩频数分布直方图;
(3)在此次测试中,某学生的成绩是87分,在他所属学校排在前10名,由表中数据可知该学生是 校的学生(填“甲”或“乙”),理由是 ;
(4)假设甲校200名学生都参加此次测试,若成绩80分及以上为优秀,估计成绩优秀的学生人数为__________.
查看答案和解析>>
科目: 来源: 题型:
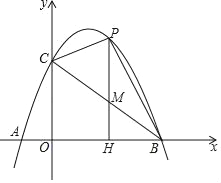
【题目】如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(﹣1,0),B(3,0)两点,与y轴相交于点C(0,3)
(1)求这个二次函数的表达式并直接写出顶点坐标;
(2)若P是第一象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.设点P的横坐标为t
①求线段PM的最大值;
②S△PBM:S△MHB=1:2时,求t值;
③当△PCM是等腰三角形时,直接写点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知y是x的函数,自变量x的取值范围是![]() ,下表是y与x的几组对应值.
,下表是y与x的几组对应值.

小华根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.下面是小华的探究过程,请将其补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象.
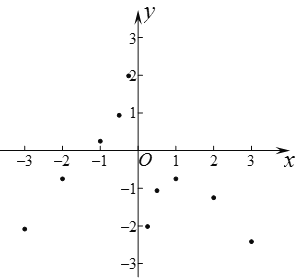
(2)根据画出的函数图象,写出:
①![]() 时,对应的函数值y约为 (结果精确到0.01);
时,对应的函数值y约为 (结果精确到0.01);
②该函数的一条性质: .
查看答案和解析>>
科目: 来源: 题型:
【题目】学校组织初二年级学生去参加社会实践活动,学生分别乘坐甲车、乙车,从学校同时出发,沿同一路线前往目的地.在行驶过程中,甲车先匀速行驶1小时后,提高速度继续匀速行驶,当甲车超过乙车40千米后停下来等候乙车,两车相遇后,甲车和乙车一起按乙车原来的速度匀速行驶到达目的地.如图是甲、乙两车行驶的全过程中经过的路程y(千米)与出发的时间x(小时)之间函数关系图象.根据图中提供的信息,解答下列问题:
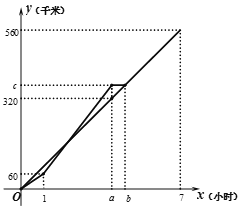
(1)甲车行驶的路程为______千米;
(2)乙车行驶的速度为______千米/时,甲车等候乙车的时间为______小时;
(3)甲、乙两车出发________小时,第一次相遇;
(4)甲、乙两车出发________小时,相距20千米.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,过点F作FG⊥BF交BC的延长线于点G.
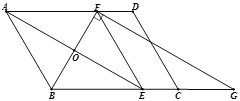
(1)求证:四边形ABEF是菱形;
(2)如果AB= 2,∠BAD=60°,求FG的长.
查看答案和解析>>
科目: 来源: 题型:
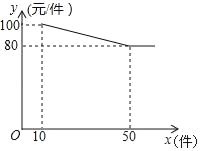
【题目】服装厂批发某种服装,每件成本为65元,规定不低于10件可以批发,其批发价y(元/件)与批发数量x(件)(x为正整数)之间所满足的函数关系如图所示.
(1)求y与x之间所满足的函数关系式,并写出x的取值范围;
(2)设服装厂所获利润为w(元),若10≤x≤50(x为正整数),求批发该种服装多少件时,服装厂获得利润最大?最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:![]() 过点A(3,0),且与直线l2:
过点A(3,0),且与直线l2:![]() 交于点B(m,1).
交于点B(m,1).
(1)求直线l1:![]() 的函数表达式;
的函数表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1、l2分别交于点C、D,当点C位于点D上方时,直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.
例如,如图1,正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
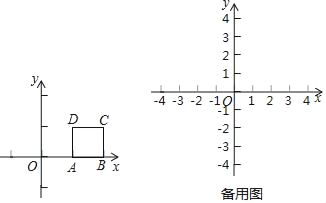
(1)如果⊙P是以(3,4)为圆心,2为半径的圆,那么点O(0,0)到⊙P的距离为 ;
(2)①求点M(3,0)到直线了y=![]() x+4的距离:
x+4的距离:
②如果点N(0,a)到直线y=![]() x+4的距离为2,求a的值;
x+4的距离为2,求a的值;
(3)如果点G(0,b)到抛物线y=x2的距离为3,请直接写出b的值.
查看答案和解析>>
科目: 来源: 题型:
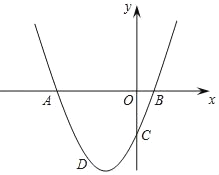
【题目】已知,抛物线y=ax2+2ax+c与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)当a>0时,如图所示,若点D是第三象限方抛物线上的动点,设点D的横坐标为m,三角形ADC的面积为S,求出S与m的函数关系式,并直接写出自变量m的取值范围;请问当m为何值时,S有最大值?最大值是多少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com