
科目: 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点O为正方形ABCD 的中心,E为AB 边上一点,F为BC边上一点,△EBF的周长等于 BC 的长.
(1)求∠EOF 的度数.
(2)连接 OA、OC(如图2).求证:△AOE∽△CFO.
(3)若OE=![]() OF,求
OF,求![]() 的值.
的值.

查看答案和解析>>
科目: 来源: 题型:
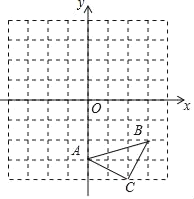
【题目】如图,△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),在正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移4个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C,使△A2B2C与△ABC位似,且△A2B2C与△ABC的位似比为2:1,并直接写出点B2的坐标.
查看答案和解析>>
科目: 来源: 题型:
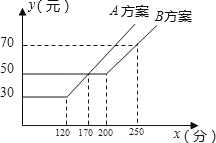
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目: 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】盒子中有4个球,每个球上写有1~4中的一个数字,不同的球上数字不同.
(1)若从盒中取三个球,以球上所标数字为线段的长,则能构成三角形的概率是多少?
(2)若小明从盒中取出一个球,放回后再取出一个球,然后让小华猜两球上的数字之和,你认为小华猜和为多少时,猜中的可能性大.请说明理由.
查看答案和解析>>
科目: 来源: 题型:
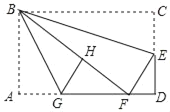
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
查看答案和解析>>
科目: 来源: 题型:
【题目】宽与长的比是![]() (约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC的平分线,交AD的延长线于点H,作HG⊥BC,交BC的延长线于点G,则下列矩形是黄金矩形的是( )
(约为0.618)的矩形叫做黄金矩形,黄金矩形蕴藏着丰富的美学价值,给我们以协调和匀称的美感.我们可以用这样的方法画出黄金矩形:如图,作正方形ABCD,分别取AD,BC的中点E,F,连接EF,DF,作∠DFC的平分线,交AD的延长线于点H,作HG⊥BC,交BC的延长线于点G,则下列矩形是黄金矩形的是( )
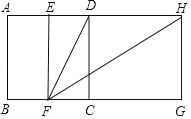
A.矩形ABFEB.矩形EFCDC.矩形EFGHD.矩形DCGH
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com