
科目: 来源: 题型:
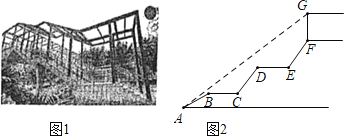
【题目】为了方便学生在上下学期间安全过马路,南岸区政府决定在南开(融侨)中学校门口修建人行天桥(如图1),其平面图如图2所示,初三(8)班的学生小刘想利用所学知识测量天桥顶棚距地面的高度.天桥入口A点有一台阶AB=2m,其坡角为30°,在AB上方有两段平层BC=DE=1.5m,且BC,DE与地面平行,BC,DE上方又紧接台阶CD,EF,其长度相等且坡度均为i=4:3,顶棚距天桥距离FG=2m,且小刘从入口A点测得顶棚顶端G的仰角为37°,请根据以上数据,帮小刘计算出顶端G点距地面高度为( )m.(结果保留一位小数,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
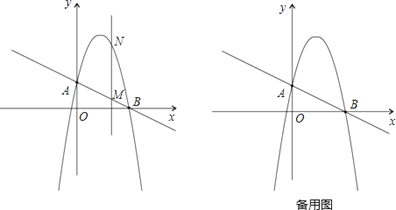
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)探究发现:下面是一道例题及解答过程,请补充完整:
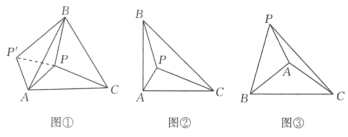
如图①在等边△ABC内部,有一点P,若∠APB=150°,求证:AP2+BP2=CP2
证明:将△APC绕A点逆时针旋转60°,得到△AP’B,连接PP’,则△APP’为等边三角形
∴∠APP’=60° ,PA=PP’ ,PC=
∵∠APB=150°,∴∠BPP’=90°
∴P’P2+BP2= ,即PA2+PB2=PC2
(2)类比延伸:如图②在等腰△ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA,PB,PC之间的数量关系,并证明.
(3)联想拓展:如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2(其中k>0),请直接写出k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如果关于x的一元二次方程![]() (a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程
(a≠0)有两个不相等的实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,方程![]() 的两个根是2和4,则方程
的两个根是2和4,则方程![]() 就是“倍根方程”.
就是“倍根方程”.
(1)若一元二次方程![]() 是“倍根方程”,则c=
是“倍根方程”,则c=
(2)若方程![]() (a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线
(a≠0)是倍根方程,且相异两点M(1+t,s),N(4-t,s),都在抛物线![]() 上,求一元二次方程
上,求一元二次方程![]() (a≠0)的根.
(a≠0)的根.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

查看答案和解析>>
科目: 来源: 题型:
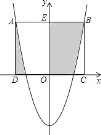
【题目】已知二次函数y=2x2+m.(1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_________y2(填“>”、“=”或“<”);(2)如图,此二次函数的图象经过点(0,-4),正方形ABCD的顶点C、D在x轴上,A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).

(1)将△AOB向下平移3个单位后得到△A1O1B1,则点B1的坐标为 ;
(2)将△AOB绕点O逆时针旋转90°后得到△A2OB2,请在图中作出△A2OB2,并求出这时点A2的坐标为 ;
(3)在(2)中的旋转过程中,线段OA扫过的图形的面积 .
查看答案和解析>>
科目: 来源: 题型:
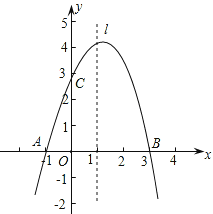
【题目】已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;
(3)在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com